Peras Technical Report #2

The goal of this document is to provide a detailed analysis of the Peras protocol from an engineering point of view, based upon the work done by the Innovation team between April and July 2024. It is based on the pre-alpha version of the protocol as designed by the Research team.

Executive summary

This section lists a number of findings, conclusions, ideas, and known risks that we have garnered as part of the Peras innovation project. Overall, work on the Peras protocol has matured to Software Readiness Level (SRL) 4 and, although a few aspects of the innovation project require completion and polish, the post-innovation roadmapping and processes can proceed.

Product

We have refined our analysis and understanding of Peras protocol, taking into account its latest evolution:

• A promising solution for votes and certificates construction has been identified based on existing VRF/KES keys and ALBAs certificates.
  • This solution relies on existing nodes' infrastructure and cryptographic primitives and therefore should be straightforward to implement and deploy.
• Peras's votes and certificates handling will have a negligible impact on existing node CPU, network bandwidth, and memory requirements.
  • They will have a moderate impact on storage requirements leading to a potential increase of disk storage of 15 to 20%..
  • Peras might have a moderate economical impact for SPOs running their nodes with cloud providers due to increasing network egress traffic.
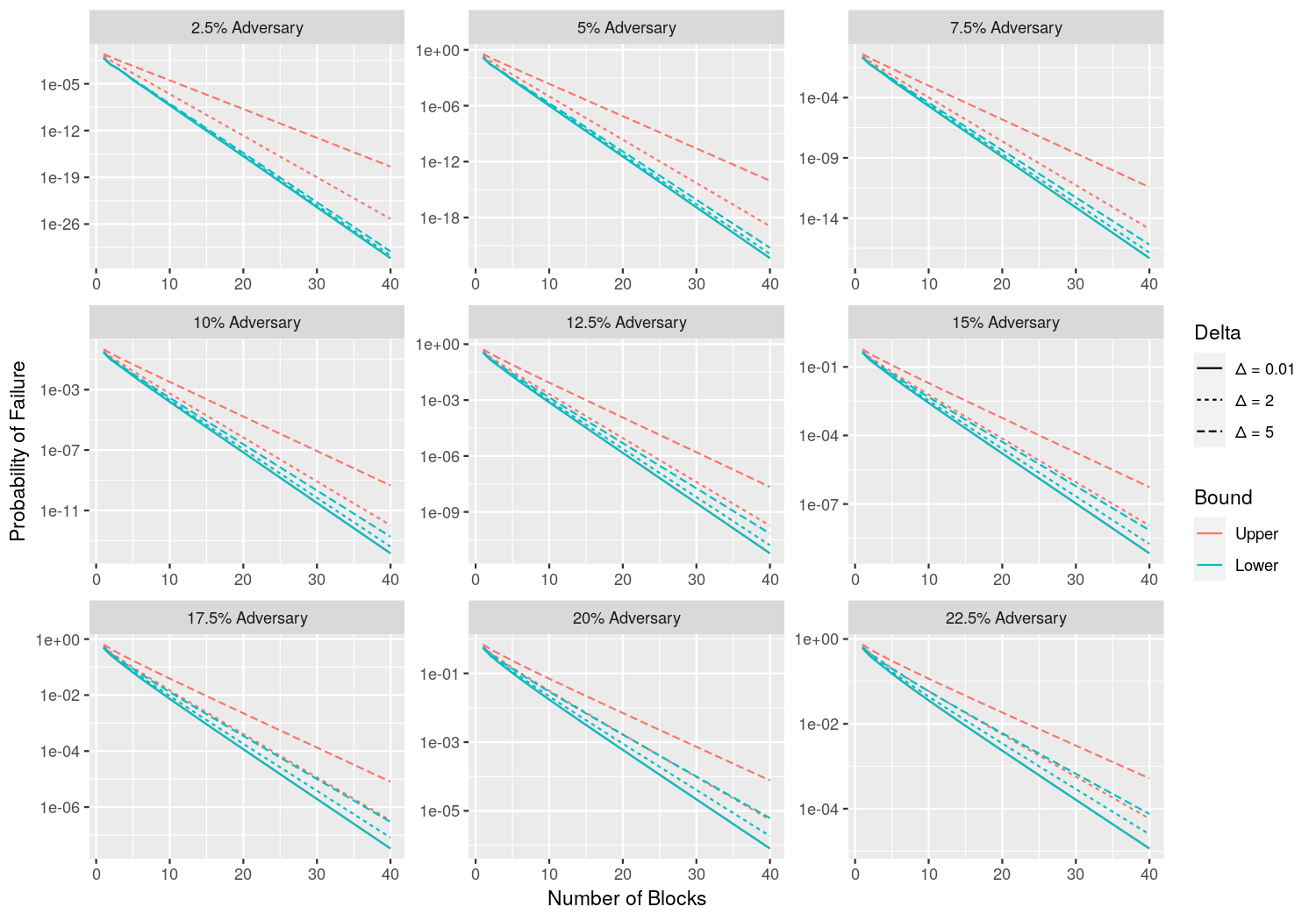
• Peras's impact on settlement probabilities depends strongly upon the specific choices for protocol parameters and upon which stakeholder use case(s) those have been tuned for.
  • Settlement can be as fast as two minutes, with an infinitesimal probability of rollback after that, but there is an appreciable probability of rollback prior to that time if a strong adversary attacks.
  • Stakeholders will have to reach consensus about the relative importance of settlement time versus pre-settlement resistance to attacks.
• We think development of a pre-alpha prototype integrated with the cardano-node should be able to proceed.

Process

The following pictures shows how our R&D process evolved over the course of the past few months.

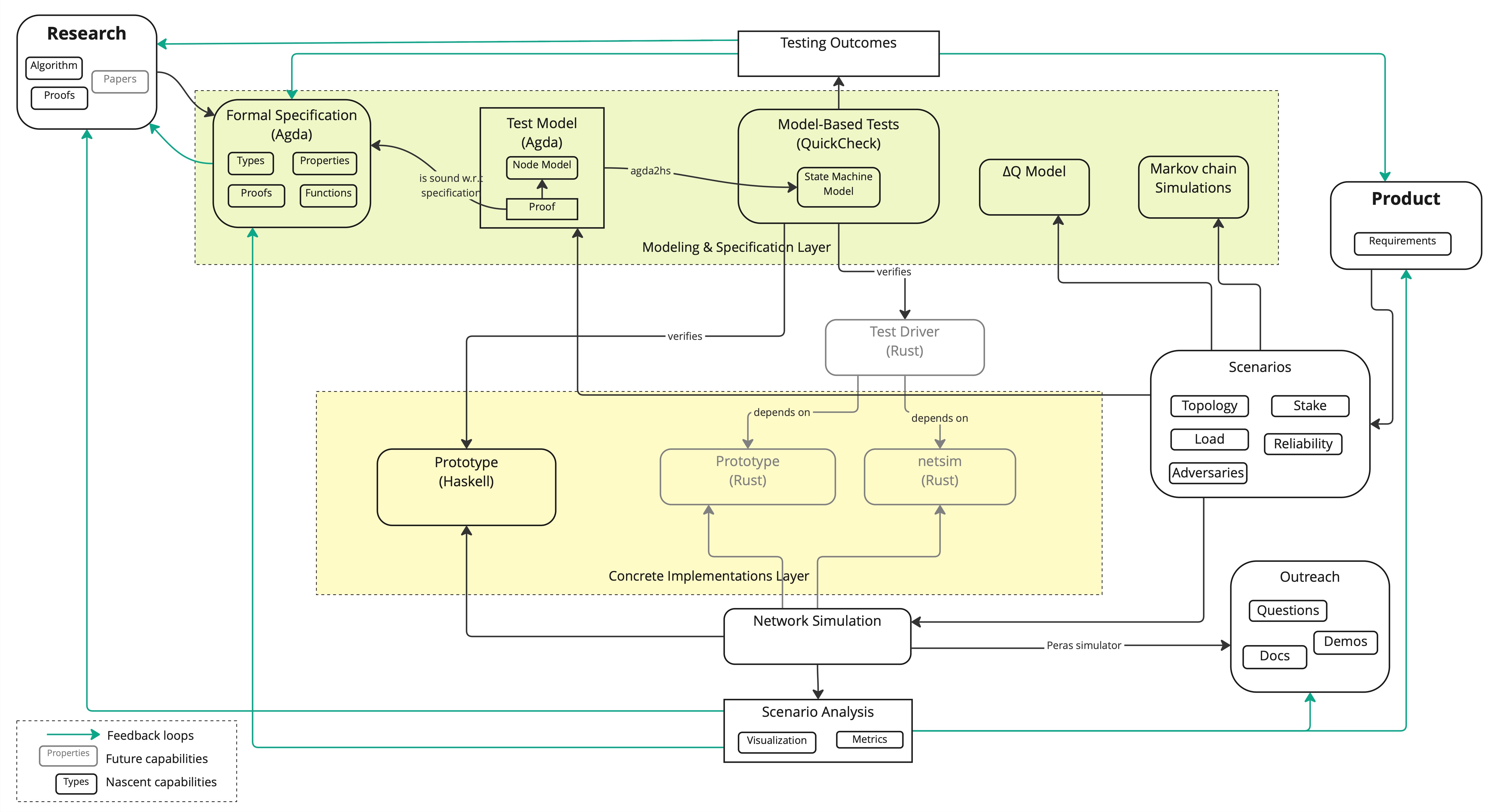
• Formal specification work has focused on aligning with pre-alpha version of the protocol and writing safety proofs for Peras using a characteristic string technique similar to the one used in various Praos-related papers.
• The link between the Formal specification and implementation through Conformance tests has been strengthened thanks to fruitful collaboration with Quviq:
  • The Test model aka executable specification is defined in Agda then projected to Haskell for direct reuse by quickcheck-dynamic execution engine.
  • A Soundness proof ensures that it is consistent with the (higher level) formal specification.
  • We have not yet covered adversarial behavior but most scenarios should be straightforward to implement.
• We have discontinued Rust prototype support, from want of time, but we have not changed how tests are run so we have strong confidence any implementation with a compatible API should be testable.
• We have built a user-facing simulation tool that proved helpful to better understand the protocol's behavior, spot potential issues, and align all stakeholders over an unambiguous prototype.
• We have built analytic and Markov-chain models to simulate various interesting large scale behaviors of Peras probabilistically, providing a wealth of insights on parameters interaction and performance in response to adversarial conditions.
• We have continued investigating the use of ΔQ formalism, trying to leverage more recent implementations for modelling vote diffusion.
• We have documented constraints on the Peras protocol parameters and recommended interim default values for them.
• While there remain some work to be done on that front, we should be able to make this Peras work, including the present report and interactive tools, fully public.

Introduction

Software readiness level

We use Software Technology Readiness Level as a crude assessment of how far we are in the journey leading from an idea to actual code running in production.

In our previous technical report we estimated having reached SRL 3:

Questions to resolve	Status
Critical functions/components of the concept/application identified?	Done
Subsystem or component analytical predictions made?	Done
Subsystem or component performance assessed by Modeling and Simulation?	Done
Preliminary performance metrics established for key parameters?	Done
Laboratory tests and test environments established?	Done
Laboratory test support equipment and computing environment completed for component/proof-of-concept testing?	N/A
Component acquisition/coding completed?	Partial
Component verification and validation completed?	Mostly
Analysis of test results completed establishing key performance metrics for components/ subsystems?	Done
Analytical verification of critical functions from proof-of-concept made?	Done
Analytical and experimental proof-of-concept documented?	Done

At the date of publication for this report, we have reached SRL 4:

Questions to resolve	Status
Concept/application translated into detailed system/subsystem/component level software architecture design?	Partial
Preliminary definition of operational environment completed?	Done
Laboratory tests and test environments defined for integrated component testing?	Partial
Pre-test predictions of integrated component performance in a laboratory environment assessed by Modeling and Simulation?	Done
Key parameter performance metrics established for integrated component laboratory tests?	Done
Laboratory test support equipment and computing environment completed for integrated component testing?	Partial
System/subsystem/component level coding completed?	Partial
Integrated component tests completed?	Partial
Analysis of test results completed verifying performance relative to predictions?	Done
Preliminary system requirements defined for end users' application?	Done
Critical test environments and performance predictions defined relative operating environment?	Done
Relevant test environment defined?	Done
Integrated component tests completed for reused code?	Done
Integrated component performance results verifying analytical predictions and definition of relevant operational environment documented?	Done

Relevant documents:

document	status
Detailed Design Document	Partial
Formal Specification	Done
Proofs	Done
Simulations	Done

Protocol definition

The following is an informal specification of the protocol using some mathematical notations that we will refer to across this document. The detailed formal specification can be found here, and the reference implementation in Haskell is available in GitHub.

Variables

The protocol keeps track of the following variables, initialized to the values below:

• In1: $C_\text{pref} \gets C_\text{genesis}$: preferred chain;
• In2: $\mathcal{C} \gets \{C_\text{genesis}\}$: set of chains;
• In3: $\mathcal{V} \gets \emptyset$: set of votes;
• In4: $\mathsf{Certs} \gets \{\mathsf{cert}_\text{genesis}\}$: set of certificates;
• In5: $\mathsf{cert}^\prime \gets \mathsf{cert}_\text{genesis}$: the latest certificate seen;
• In6: $\mathsf{cert}^* \gets \mathsf{cert}_\text{genesis}$: the latest certificate on chain.

Sequence

The protocol operations occur sequentially in the following order:

• Fetching
• Block Creation
• Voting

Fetching

At the beginning of each slot:

• Fe1: Fetch new chains $\mathcal{C}_\text{new}$ and votes $\mathcal{V}_\text{new}$.
• Fe2: Add any new chains in $\mathcal{C}_\text{new}$ to $\mathcal{C}$, add any new certificates contained in chains in $\mathcal{C}_\text{new}$ to $\mathsf{Certs}$.
  • Fe2x: Discard any equivocated blocks or certificates: i.e., do not add them to $\mathcal{C}$ or $\mathsf{Certs}$.
• Fe3: Add $\mathcal{V}_\text{new}$ to $\mathcal{V}$ and turn any new quorum in $\mathcal{V}$ into a certificate $\mathsf{cert}$ and add $\mathsf{cert}$ to $\mathsf{Certs}$.
  • Fe3x: Discard any equivocated votes: i.e., do not add the to $\mathcal{V}$.
• Fe4: Set $C_\text{pref}$ to the heaviest (w.r.t. $\mathsf{Wt}_\mathsf{P}(\cdot)$) valid chain in $\mathcal{C}$.
  • Fe4x: If several chains have the same weight, select the one whose tip has the smallest block hash as the preferred one.
  • Each party $\mathsf{P}$ assigns a certain weight to every chain $C$, based on $C$'s length and all certificates that vote for blocks in $C$ that $\mathsf{P}$ has seen so far (and thus stored in a local list $\mathsf{Certs}$).
  • CW1: Let $\mathsf{certCount}_\mathsf{P}(C)$ denote the number of such certificates, i.e., $\mathsf{certCount}_\mathsf{P}(C) := \left| \left\{ \mathsf{cert} \in \mathsf{Certs} : \mathsf{cert} \text{ votes for a block on } C \right\} \right|$.
  • CW2: Then, the weight of the chain $C$ in $\mathsf{P}$'s view is $\mathsf{Wt}_\mathsf{P}(C) := \mathsf{len}(C) + B \cdot \mathsf{certCount}_\mathsf{P}(C)$ for a protocol parameter $B$.
• Fe5: Set $\mathsf{cert}^\prime$ to the certificate with the highest round number in $\mathsf{Certs}$.
• Fe6: Set $\mathsf{cert}^*$ to the certificate with the highest round number on (i.e., included in) $C_\text{pref}$.

Block creation

Whenever party $\mathsf{P}$ is slot leader in a slot $s$, belonging to some round $r$:

• BC1: Create a new block $\mathsf{block} = (s, \mathsf{P}, h, \mathsf{cert}, ...)$, where
  • BC2: $h$ is the hash of the last block in $C_\text{pref}$,
  • BC3: $\mathsf{cert}$ is set to $\mathsf{cert}^\prime$ if
    • BC4: there is no round-$(r-2)$ certificate in $\mathsf{Certs}$, and
    • BC5: $r - \mathsf{round}(\mathsf{cert}^\prime) \leq A$, and
    • BC6: $\mathsf{round}(\mathsf{cert}^\prime) > \mathsf{round}(\mathsf{cert}^*)$,
    • BC7: and to $\bot$ otherwise,
• BC8 Extend $C_\text{pref}$ by $\mathsf{block}$, add the new $C_\text{pref}$ to $\mathcal{C}$ and diffuse it.

Voting

Party $\mathsf{P}$ does the following at the beginning of each voting round $r$:

• Vo1: Let $\mathsf{block}$ be the youngest block at least $L$ slots old on $C_\text{pref}$.
• Vo2: If party $\mathsf{P}$ is (voting) committee member in a round $r$,
  • either
    • VR-1A: $\mathsf{round}(\mathsf{cert}^\prime) = r-1$ and $\mathsf{cert}^\prime$ was received before the end of round $r-1$, and
    • VR-1B: $\mathsf{block}$ extends (i.e., has the ancestor or is identical to) the block certified by $\mathsf{cert}^\prime$,
  • or
    • VR-2A: $r \geq \mathsf{round}(\mathsf{cert}^\prime) + R$, and
    • VR-2B: $r = \mathsf{round}(\mathsf{cert}^*) + c \cdot K$ for some $c > 0$,
  • Vo3: then create a vote $v = (r, \mathsf{P}, h,...)$,
  • Vo4: Add $v$ to $\mathcal{V}$ and diffuse it.

Votes & certificates

This section details the Peras voting process, from the casting and detailed structure of votes, to the creation, diffusion, and storage of certificates.

Votes

Overview

Voting in Peras is mimicked after the sortition algorithm used in Praos, e.g it is based on the use of a Verifiable Random Function (VRF) by each stake-pool operator guaranteeing the following properties:

• The probability for each voter to cast their vote in a given round is correlated to their share of total stake,
• It should be computationally impossible to predict a given SPO's schedule without access to their secret key VRF key,
• Verification of a voter's right to vote in a round should be efficiently computable,
• A vote should be unique and non-malleable. (This is a requirement for the use of efficient certificates aggregation, see below.)

Additionally we would like the following property to be provided by our voting scheme:

• Voting should require minimal additional configuration (i.e., key management) for SPOs,
• Voting and certificates construction should be fast in order to ensure we do not interfere with other operations happening in the node.

We have experimented with two different algorithms for voting, which we detail below.

Structure of votes

We have used an identical structure for single Votes, for both algorithms. We define this structure as a CDDL grammar, inspired by the block header definition from cardano-ledger:

vote =
  [ voter_id         : hash32
  , voting_round     : round_no
  , block_hash       : hash32
  , voting_proof     : vrf_cert
  , voting_weight    : voting_weight
  , kes_period       : kes_period
  , kes_vkey         : kes_vkey
  , kes_signature    : kes_signature
  ]

This definition relies on the following primitive types (drawn from Ledger definitions in crypto.cddl)

round_no = uint .size 8
voting_weight = uint .size 8
vrf_cert = [bytes, bytes .size 80]
hash32 = bytes .size 32
kes_vkey = bytes .size 32
kes_signature = bytes .size 448
kes_period = uint .size 8

As already mentioned, Vote mimicks the block header's structure which allows Cardano nodes to reuse their existing VRF and KES keys. Some additional notes:

• Total vote size is 710 bytes with the above definition,
• Unless explicitly mentioned, hash function exclusively uses 32-bytes Blake2b-256 hashes,
• The voter_id is it's pool identifier, ie. the hash of the node's cold key.

Casting vote

A vote is cast by a node using the following process which paraphrases the actual code

1. Define nonce as the hash of the epoch nonce concatenated to the peras string and the round number voted for encoded as 64-bits big endian value,
2. Generate a VRF Certificate using the node's VRF key from this nonce,
3. Use the node's KES key with current KES period to sign the VRF certificate concatenated to the block hash the node is voting for,
4. Compute voting weight from the VRF certificate using sortition algorithm (see details below).

Verifying vote

Vote verification requires access to the current epoch's stake distribution and stake pool registration information.

1. Lookup the voter_id in the stake distribution and registration map to retrieve their current stake and VRF verification key,
2. Compute the nonce (see above),
3. Verify VRF certificate matches nonce and verification key,
4. Verify KES signature,
5. Verify provided KES verification key based on stake pool's registered cold verification key and KES period,
6. Verify provided voting weight according to voting algorithm.

Leader-election like voting

The first algorithm is basically identical to the one used for Mithril signatures, and is also the one envisioned for Leios (see Appendix D of the recent Leios paper). It is based on the following principles:

• The goal of the algorithm is to produce a number of votes targeting a certain threshold such that each voter receives a number of vote proportionate to $\sigma$, their fraction of total stake, according to the basic probability function $\phi(\sigma) = 1 - (1 - f)^\sigma$,
• There are various parameters to the algorithm:
  • $f$ is the fraction of slots that are "active" for voting
  • $m$ is the number of lotteries each voter should try to get a vote for,
  • $k$ is the target total number of votes for each round (e.g., quorum) $k$ should be chosen such that $k = m \cdot \phi(0.5)$ to reach a majority quorum,
• When its turn to vote comes, each node run iterates over an index $i \in [1 \dots m]$, computes a hash from the nonce and the index $i$, and compares this hash with $f(\sigma)$: if it is lower than or equal, then the node has one vote.
  • Note the computation $f(\sigma)$ is exactly identical to the one used for leader election.

We prototyped this approach in Haskell.

Sortition-like voting

The second algorithm is based on the sortition process initially invented by Algorand and implemented in their node. It is based on the same idea, namely that a node should have a number of votes proportional to their fraction of total stake, given a target "committee size" expressed as a fraction of total stake $p$. And it uses the fact the number of votes a single node should get based on these parameters follows a binomial distribution.

The process for voting is thus:

• Compute the individual probability of each "coin" to win a single vote $p$ as the ratio of expected committee size over total stake.
• Compute the binomial distribution $B(n,p)$ where $n$ is the node's stake.
• Compute a random number between 0 and 1 using nonce as the denominator over maximum possible value (e.g., all bits set to 1) for the nonce as denominator.
• Use bisection method to find the value corresponding to this probability in the CDF for the aforementioned distribution.

This yields a vote with some weight attached to it "randomly" computed so that the overall sum of weights should be around expected committee size.

This method has also been prototyped in Haskell.

Benchmarks

The peras-vote package provides some benchmarks comparing the two approaches, which gives us:

• Single Voting (Binomial): 139.5 μs
• Single Verification (binomial): 160.9 μs
• Single Voting (Taylor): 47.02 ms

note

The implementation takes some liberty with the necessary rigor suitable for cryptographic code, but the timings provided should be consistent with real-world production grade code. In particular, when using nonce as a random value, we only use the low order 64 bits of the nonce, not the full 256 bits.

Certificates

Mithril certificates

Mithril certificates' construction is described in details in the Mithril paper and is implemented in the mithril network. It's also described in the Leios paper, in the appendix, as a potential voting scheme for Leios, and implicitly Peras.

Mithril certificates have the following features:

• They depend on BLS-curve signatures aggregation to produce a so-called State based Threshold Multi-Signature that's easy to verify,
• Each node relies on a random lottery as described in the previous section to produce a vote weighted by their share of total stake,
• The use of BLS signatures implies nodes will need to generate and exchange specialized keys for the purpose of voting, something we know from Mithril is somewhat tricky as it requires some form of consensus to guarantee all nodes have the exact same view of the key set.

ALBA

danger

2024-10-07 Update

On closer scrutiny, it appeared the parameters used in these benchrmarks are way too optimistic, which lead us to conclude hastily ALBA would be the "right" certificate scheme for Peras. Actually, to provide strong guarantees about quorum, the $n_f$ parameter should be set to the quorum value, e.g 75% of stake, which means the $n_p$ should be set quite high too as certificate size is pretty much dependent on the $n_p/n_f$ ratio.

A thorough analysis of the issues is discussed on the ALBA repository, thanks to Alex Esgen for pointing it out.

Approximate Lower Bound Arguments or ALBAs in short, are a novel cryptographic algorithm based on a telescope construction providing a fast way to build compact certificates out of a large number of unique items. A lot more details are provided in the paper, on the website and the GitHub repository where implementation is being developed, we only provide here some key information relevant to the use of ALBAs in Peras.

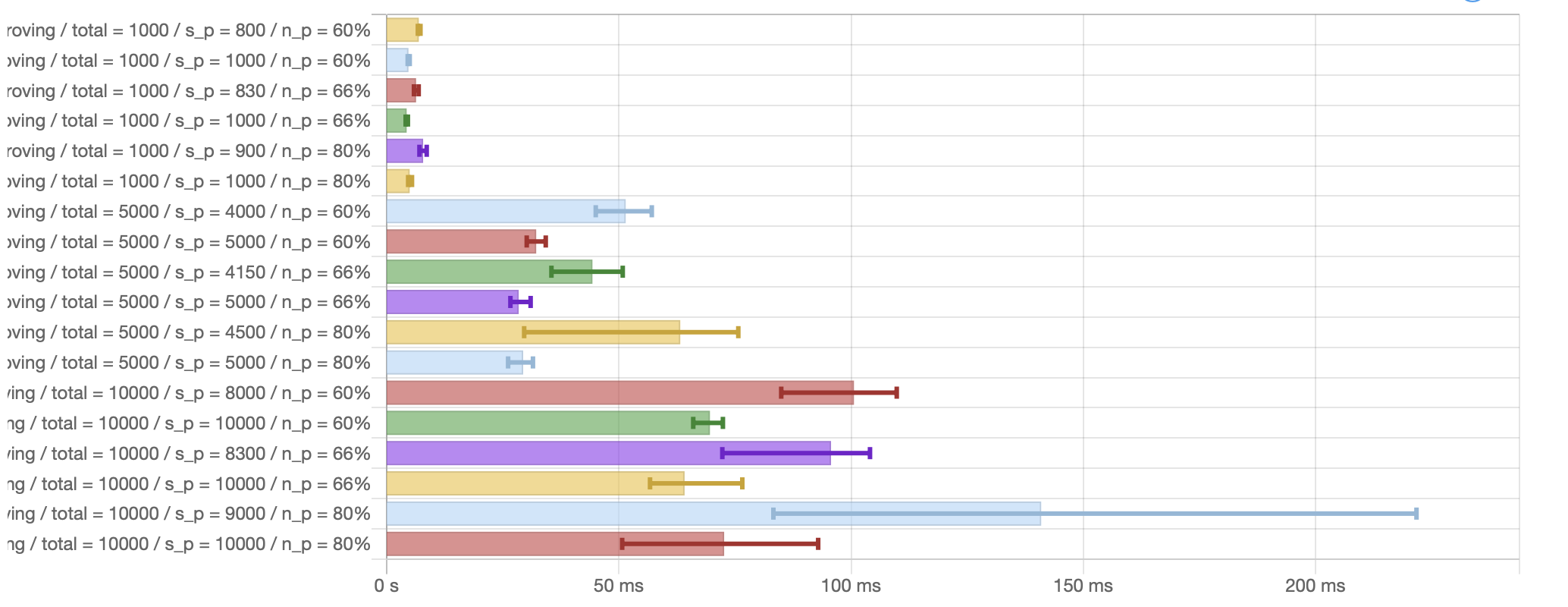
Proving & verification time

ALBA's expected proving time is benchmarked in the following picture which shows mean execution time for generating a proof depending on: The total number of votes, the actual number of votes ($s_p$), the honest ratio ($n_p$). Note that as proving time increases exponentially when $s_p \rightarrow total \cdot n_p$, we only show here the situation when $s_p = total$ and $s_p = total - total \cdot n_p / 2$ to ensure graph stays legible.

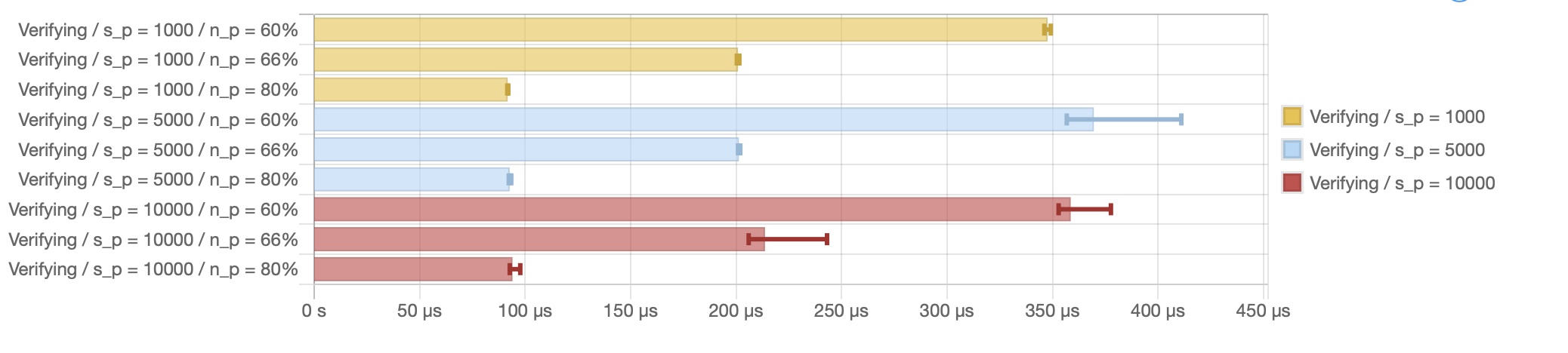
The following diagram is an excerpt from the ALBA benchmarks highlighting verification. Note these numbers do not take into account the time for verifying individual votes. As one can observe directly from these graphs, verification time is independent from the number of items and only depends on the $n_p/n_f$ ratio.

In practice, as the number of votes is expected to be in the 1000-2000 range, and there is ample time in a round to guarantee those votes are properly delivered to all potential voting nodes (see below), we can safely assume proving time of about 5 ms, and verification time under a millisecond.

Certificate size

For a given set of parameters, namely fixed values for $\lambda_{sec}$, $\lambda_{rel}$, and $n_p/n_f$, the proof size is perfectly linear and only depends on the size of each vote.

Varying the security parameter and the honest votes ratio for a fixed set of 1000 votes of size 200 yields the following diagram, showing the critical factor in proof size increase is the $n_p/n_f$ ratio: As this ratio decreases, the number of votes to include in proof grows superlinearly.

Benchmarks

In the following tables we compare some relevant metrics between the two different kind of certificates we studied, Mithril certificates (using BLS signatures) and ALBA certificates (using KES signatures): Size of certificate in bytes, proving time (e.g., the time to construct a single vote), aggregation time (the time to build a certificate), and verification time.

For Mithril certificates, assuming parameters similar to mainnet's ($k=2422, m=20973, f=0.2$):

Feature	Metric
Certificate size	56 kB
Proving time (per vote)	~70 ms
Aggregation time	1.2 s
Verification time (certificate)	17 ms

For ALBA certificates, assuming 1000 votes, a honest to faulty ratio of 80/20, and security parameter $λ=128$. Note the proving time does not take into account individual vote verification time, whereas certificate's verification time includes votes verification time.

Feature	Metric
Certificate size	47 kB
Proving time (per vote)	~133 us
Aggregation time	~5 ms
Verification time (certificate)	15 ms

Vote diffusion

Building on previous work, we built a ΔQ model to evaluate the expected delay to reach quorum. The model works as follows:

• We start from a base uniform distribution of single MTU latency between 2 nodes, assuming a vote fits in a single TCP frame. The base latencies are identical as the one used in previous report.
• We then use the expected distribution of paths length for a random graph with 15 average connections, to model the latency distribution across the network, again reusing previously known values.
• We then apply the NToFinish 75 combinator to this distribution to compute the expected distribution to reach 75% of the votes (quorum).
• An important assumption is that each vote diffusion across the network is expected to be independent from all other votes.
• Verification time for a single vote is drawn from the above benchmarks, but we also want to take into account the verification time of a single vote, which we do in two different ways:
  • One distribution assumes a node does all verifications sequentially, one vote at a time
  • Another assumes all verifications can be done in parallel
  • Of course, the actual verification time should be expected to be in between those 2 extremes

Using the "old" version of ΔQ library based on numerical (e.g., Monte-Carlo) sampling, yields the following graph:

This graph tends to demonstrate vote diffusion should be non-problematic, with a quorum expected to be reached in under 1 second most of the time to compare with a round length of about 2 minutes.

About ΔQ libraries

At the time of this writing, a newer version of the ΔQ library based on piecewise polynomials is available. Our attempts to use it to model votes diffusion were blocked by the high computational cost of this approach and the time it takes to compute a model, specifically about 10 minutes in our case. The code for this experiment is available as a draft PR #166.

In the old version of ΔQ based on numerical sampling, which have vendored in our codebase, we introduced a NToFinish combinator to model the fact we only take into account some fraction of the underlying model. In our case, we model the case where we only care about the first 75% of votes that reach a node.

Given convolutions are the most computationally intensive part of a ΔQ model, it seems to us a modeling approach based on discrete sampling and vector/matrices operations would be quite efficient. We did some experiment in that direction, assessing various approaches in Haskell: A naive direct computation using Vectors, FFT-based convolution using vectors, and hmatrix' convolution function.

This quick-and-dirty spike lead us to believe we could provide a fast and accurate ΔQ modelling library using native vector operations provided by all modern architectures, and even scale to very large model using GPU libraries.

Simulating Peras

Protocol simulation

The Peras simulator is a prototype/reference implementation of the Peras protocol in Haskell. The implementation aims to encode the pseudo-code for the protocol specification in as literal and transparent a manner as possible, regardless of the performance drawbacks of such literalness. Note that it simulates the Peras protocol in the abstract and does not include a simulation of network diffusion. Its core contains four modules:

• Peras.Prototype.Fetching handles the receipt of new chains and new votes. It includes the following logic:
  • creates new certificates when a new quorum of votes is reached,
  • selects the preferred chain, and
  • updates $\mathsf{cert}^\prime$ and $\mathsf{cert}^*$.
• Peras.Prototype.BlockCreation forges new blocks and, optionally, includes a certificate in the new block.
• Peras.Prototype.BlockSelection selects the block that a party will vote upon.
• Peras.Prototype.Voting casts votes.

Additional, non-core modules handle the diffusion of votes, the interactions between multiple nodes, and visualization of results. The simulator's voting behavior has been tested against the Agda-derived executable specification via the quickcheck-dynamic property-based state-machine testing framework: see Peras.Conformance.Test.

The simulator can be run from the command line or in a web browser. At the command line, one can specify the input configuration (state) of the simulation, store its output configuration, and record a trace of simulation events. The ending time of the output configuration can be edited to set it to a later time, and then the simulation can be continued by providing that edited output configuration as input to the continued simulation.

$ peras-simulate --help

peras-simulate: simulate Peras protocol

Usage: peras-simulate [--version] [--in-file FILE] [--out-file FILE]
                      [--trace-file FILE]

  This command-line tool simulates the Peras protocol.

Available options:
  -h,--help                Show this help text
  --version                Show version.
  --in-file FILE           Path to input YAML file containing initial simulation
                           configuration.
  --out-file FILE          Path to output YAML file containing final simulation
                           configuration.
  --trace-file FILE        Path to output JSON-array file containing simulation
                           trace.

The input configuration file specifies the protocol parameters, the initial state of the simulation, and the slot-leadership and committee-membership schedules for each node/party. This gives the user full control over the simulation and ensures reproducibility of the simulation results.

{
  "params":{"U":20,"A":200,"R":10,"K":17,"L":10,"τ":2,"B":10,"Δ":5},
  "start":0,
  "finish":300,
  "payloads":{},
  "parties":{
    "1":{"leadershipSlots":[2,10,25,33,39,56,71,96,101,108,109,115],"membershipRounds":[1,2,6],"perasState":{"certPrime":{"blockRef":"","round":0},"certStar":{"blockRef":"","round":0},"certs":[],"chainPref":[],"chains":[[]],"votes":[]}},
    "2":{"leadershipSlots":[12,17,33,44,50,67,75,88,105],"membershipRounds":[2,3,5,6],"perasState":{"certPrime":{"blockRef":"","round":0},"certStar":{"blockRef":"","round":0},"certs":[],"chainPref":[],"chains":[[]],"votes":[]}},
    "3":{"leadershipSlots":[5,15,42,56,71,82,124],"membershipRounds":[3,4,5,6],"perasState":{"certPrime":{"blockRef":"","round":0},"certStar":{"blockRef":"","round":0},"certs":[],"chainPref":[],"chains":[[]],"votes":[]}},
    "4":{"leadershipSlots":[8,15,21,38,50,65,127],"membershipRounds":[1,5],"perasState":{"certPrime":{"blockRef":"","round":0},"certStar":{"blockRef":"","round":0},"certs":[],"chainPref":[],"chains":[[]],"votes":[]}}
  },
  "diffuser":{"delay":0,"pendingChains":{},"pendingVotes":{}}
}

The output configuration file reveals all of the chains, votes, etc. tracked by each node/party. The trace file is a JSON array of events occurring in the simulation. The trace file can be converted to a GraphViz .dot file for visualization. Traces can also be piped into tools for real-time analysis.

Tag	Event
Protocol	new protocol parameters
Tick	new slot
NewChainAndVotes	new chains and votes received
NewCertificatesReceived	new certificates received (embedded in new chains)
NewCertificatesFromQuorum	new certificates created after new votes have been fetched
NewChainPref	node prefers a new chain
NewCertPrime	node selected a new $\mathsf{cert}^\prime$
NewCertStar	node selected a new $\mathsf{cert}^*$
ForgingLogic	logic for including a certificate in a new block
DiffuseChain	chain extended by a new block
SelectedBlock	block to be voted upon
NoBlockSelected	no block voted for
VotingLogic	logic for casting a vote
DiffuseVote	diffuse a new vote

$ peras-visualize --help

peras-visualize: visualize Peras simulation traces

Usage: peras-visualize [--version] --trace-file FILE [--dot-file FILE]

  This command-line tool visualizes Peras simulation traces.

Available options:
  -h,--help                Show this help text
  --version                Show version.
  --trace-file FILE        Path to input JSON-array file containing simulation
                           trace.
  --dot-file FILE          Path to output GraphViz DOT file containing
                           visualization.

Protocol visualization

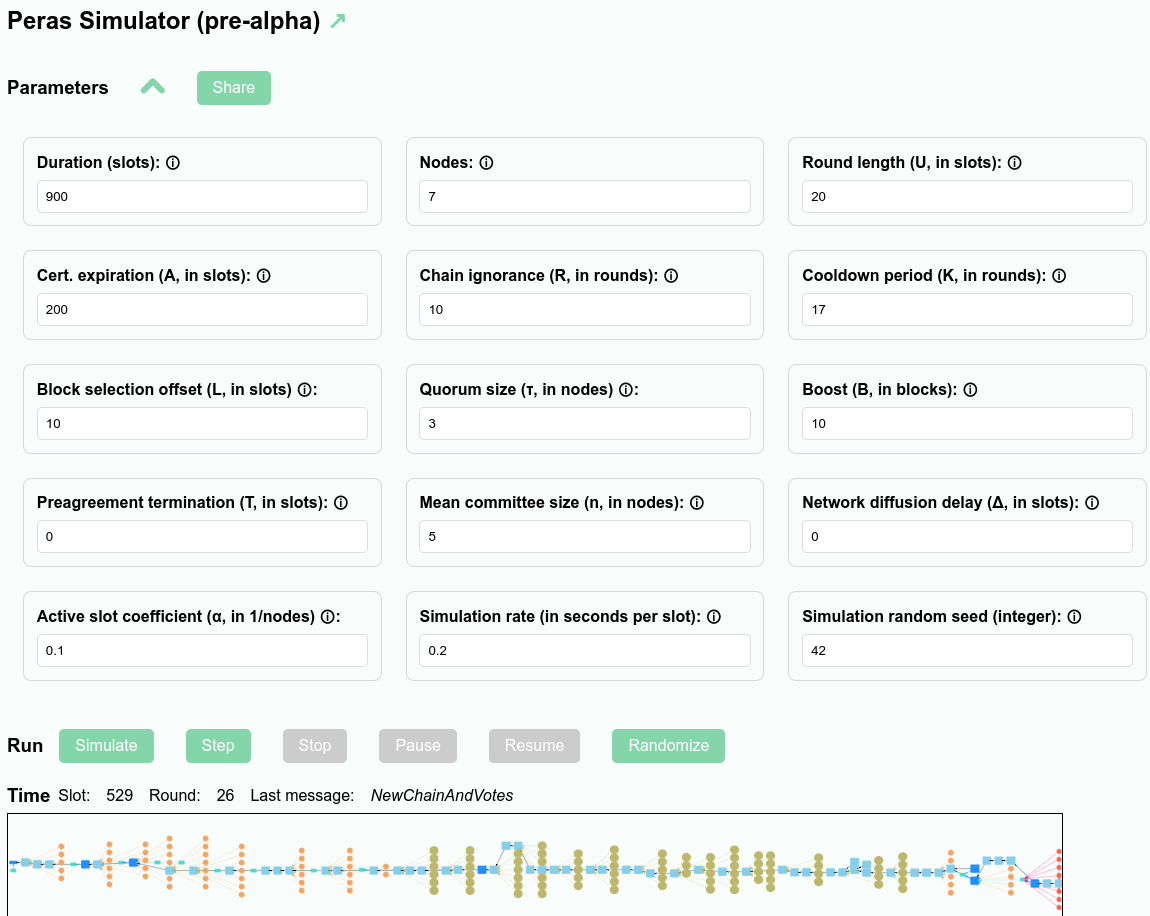
The results of simulations can be viewed graphically in a web application (see https://peras-simulation.cardano-scaling.org/) that lets one explore the operation of the Peras protocol and the influence that each of the protocol parameters has upon the evolution of the block tree. This can be used for education, for studying voting behavior, for selecting optimal values of the protocol parameters, or for debugging a simulation.

The screenshot below shows the user interface for the Peras simulation web application.

• Each of the Peras protocol parameters may be set, and tooltips provide explanations of them.
• Simulation-related parameters such as the duration of the simulation, the number of nodes involved, and the random-number seen may be set.
• Users can share simulations by copying a URL that embeds sufficient information to fully reproduce the simulation.
• Buttons allow the user to run, step singly, pause or stop the simulation.
• A zoomable display visualizes the simulated block tree.

The screenshot below shows the visualization of the Peras block tree:

• Light blue rectangles represent blocks that do not record Peras certificates, whereas dark blue rectangles represent blocks that do record Peras certificates recorded in them.
  • Block arrows point to the parent block.
  • The three ⊤ and ⊥ symbols in the block indicate whether each of the three certificate-inclusion rules are true or false, respectively.
• Salmon-colored circles represent votes for blocks, whereas olive-colored circles represent situation were a party was on the voting committee but not allowed to vote.
  • Salmon-colored dashed arrows point to the block being voted for.
  • The four ⊤ and ⊥ symbols in the block indicate whether each of the four voting rules are true or false, respectively.
• Certificates are aqua rectangles.
  • Aqua dashed arrows point to the block being certified.
• Nodes are red circles.
  • The red dashed arrows point to the tip of their preferred blockchain.
  • The orange dashed arrows point to their $\mathsf{cert}^\prime$ and $\mathsf{cert}^*$ certificates.

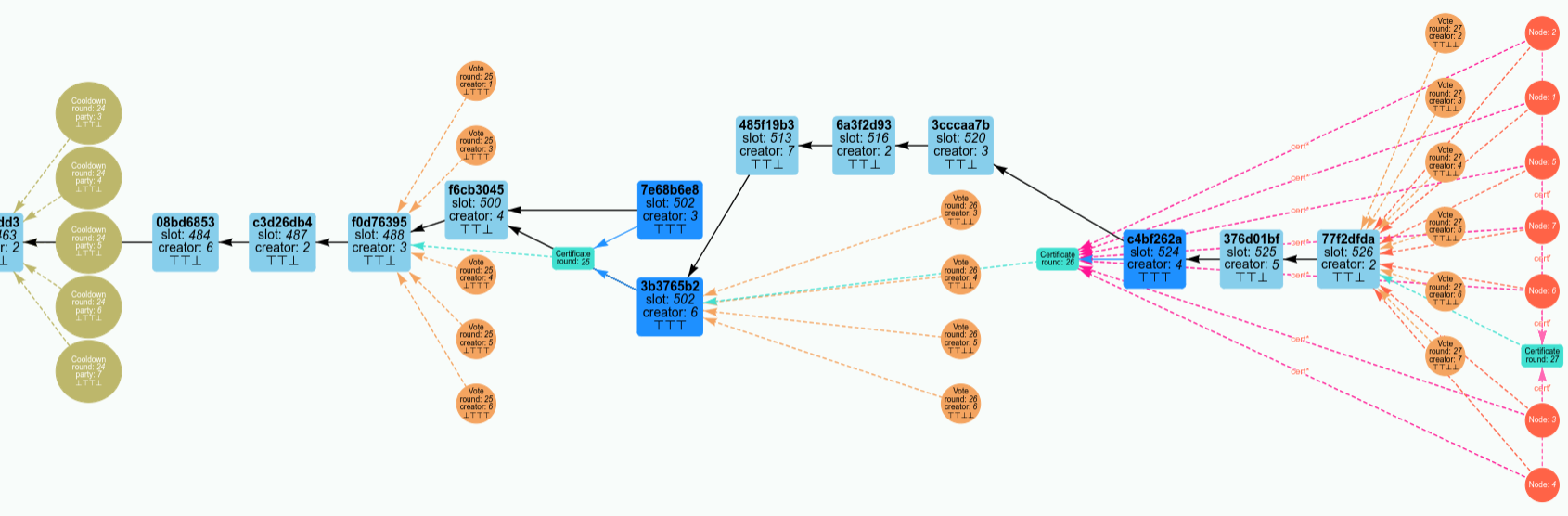
The visualizer can be deployed as a server via Docker. It supports multiple simultaneous web clients running each their own simulations and it supports basic HTTP authentication.

$ peras-server --help

peras-server: server Peras simulations

Usage: peras-server [--version] [--port PORT]
                    [--username STRING --password STRING]

  This server provides Peras simulations.

Available options:
  -h,--help                Show this help text
  --version                Show version.
  --port PORT              Port on which the server listens.
  --username STRING        Authorized user.
  --password STRING        Password for authorized user.

Markov-chain simulation

The prototype high-fidelity simulation of the Peras protocol that was presented in the previous section has the drawback that it is relatively slow because of its faithfulness to details of the protocol. The protocol operates identically (in terms of block-creation, voting, cool-down, etc.) regardless of irrelevant details such as the specific values of hashes of various object and parts of the block-tree history. Simulating the behavior of the protocol only requires a subset of the full information embedded in the objects that the protocol specifies.

Furthermore, certain significant adversarial scenarios can be approximately modeled by just considering two chains, an honest one and an adversarial one. Typically, the adversary builds their chain privately until they gain some advantage by revealing it to the honest parties. A worst-case adversarial scenario is when all the adversaries collude to build a single chain, as opposed to competing with each other by building separate adversarial chains. (Note, however, that some adversarial scenarios involve the adversaries building several "equivocated" chains in private.) In the routine course of forging blocks, honest parties might create short honest forks that are soon resolved into a preferred chain. One can idealize this process by just considering one honestly preferred chain, ignoring the short honest forks and renormalizing the probability of forging an honest block to account for the "wasted" forging of short honest forks that are quickly abandoned.

With these simplifications, one can model a Peras chain with a minimum of information required by the Protocol's logic. In the two-chain case, both the honest and adversarial parties maintain this information about their own chains.

• The current weight of the chain (i.e., length plus number of boosts)
• The round number for the block voted upon by $\mathsf{cert}^\prime$
• The pending presence of a new $\mathsf{cert}^\prime$ for the next round, if any
• The round number for the block voted upon by $\mathsf{cert}^*$
• The pending presence of a new $\mathsf{cert}^*$ for the next round, if any
• Whether there are round $r$, round $r - 1$, and/or round $r -2$ certificates

Additionally, the protocol requires tracking a few pieces of block-tree information.

• The current slot number
• The slot number for the last common prefix of the individual chains

Static values of the fraction of honest and adversarial stake result in eight constant per-slot or per-round probabilities. These are the transition probabilities of a Markov chain.

• Forging
  • No block produced in the slot
  • Only an honest block produced in the slot
  • Only an adversarial block produced in the slot
  • Both an honest and and adversarial block produced in the slot
• Voting
  • No quorum
  • Quorum of honest parties
  • Quorum of adversarial parties
  • Quorum requiring both honest and adversarial parties

Each slot that is not the start of a voting round involves a fourfold transition and each slot that is the start of a voting round involves a sixteen-fold transition. Instead of performing a Monte-Carlo simulation where only one of these four or sixteen transitions is selected according to a random variable, we can track all transitions with a data structure that assigns the cumulative probability to each outgoing state. In principle, this involves a computations on a rapidly expanding state space. In practice, however, one can prune this state space by discarding states with vanishingly small probabilities. Typically, one might discard any states with probability less than $10^{-30}$ in order to keep modest the memory footprint of the Markov-chain simulation. For Peras, this results in only having to track a million or so states, even for simulations of tens of thousands of slots.

Honest behavior proceeds according to the protocol. Adversarial behavior may differ from the protocol, but must respect the transition probabilities because those probabilities represent the incorruptible sortition rules for slot leadership or voting-committee membership. Here are some examples of easily-encoded adversarial behavior:

1. The adversary never joins honest parties in creating a quorum. Thus, the probability of no certificate being created for a round is $\mathcal{P}(\text{No quorum}) + \mathcal{P}(\text{Quorum requiring both honest and adversarial parties})$ .
2. The adversary builds their chain privately, in which case the global state variable "$\text{The slot number for the last common prefix of the individual chains}$" is never updated to reflect communication from the adversarial to the honest party.
3. The adversary builds their chain privately until it becomes weightier than the honest chain. In this case, the global state variable "$\text{The slot number for the last common prefix of the individual chains}$" and the honest chain would be updated occasionally, indicating honest parties adopt the adversarial chain when it is visibly weightier.

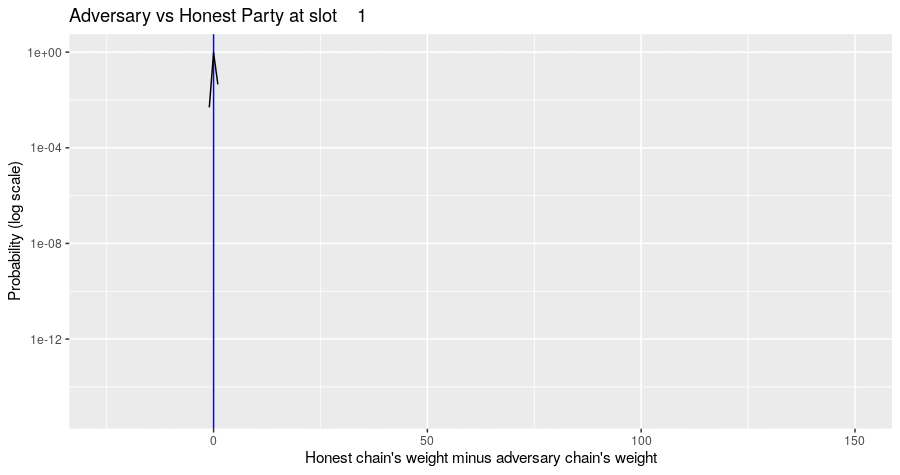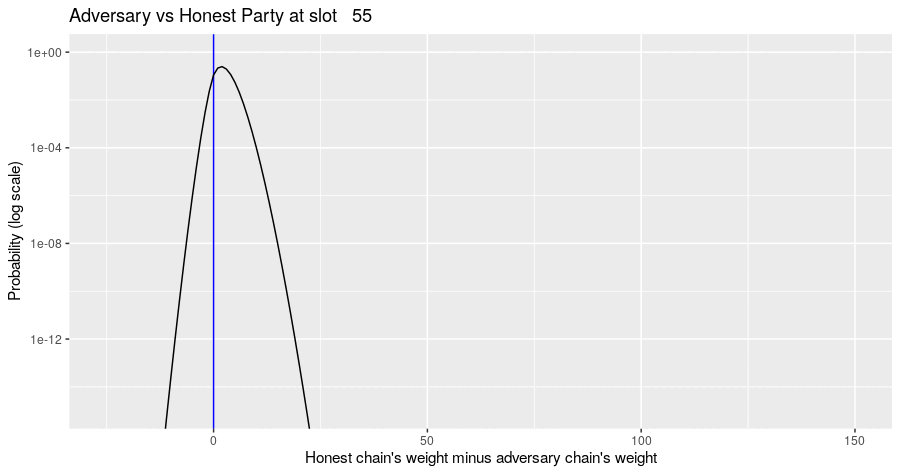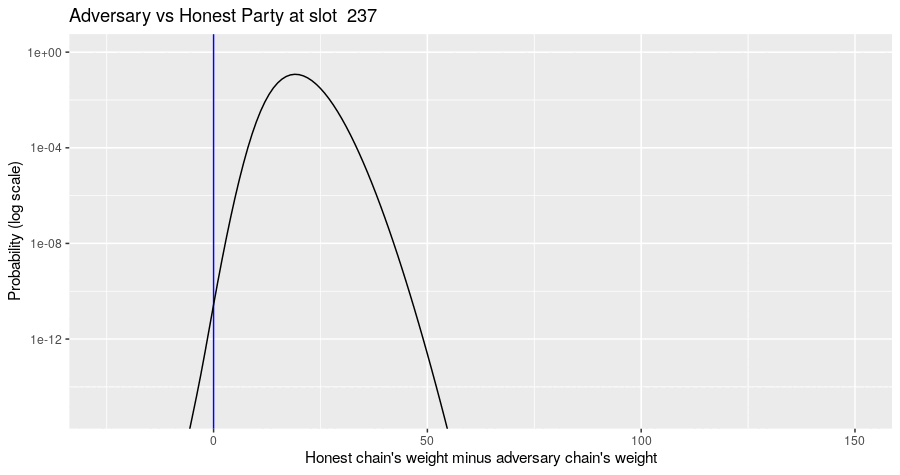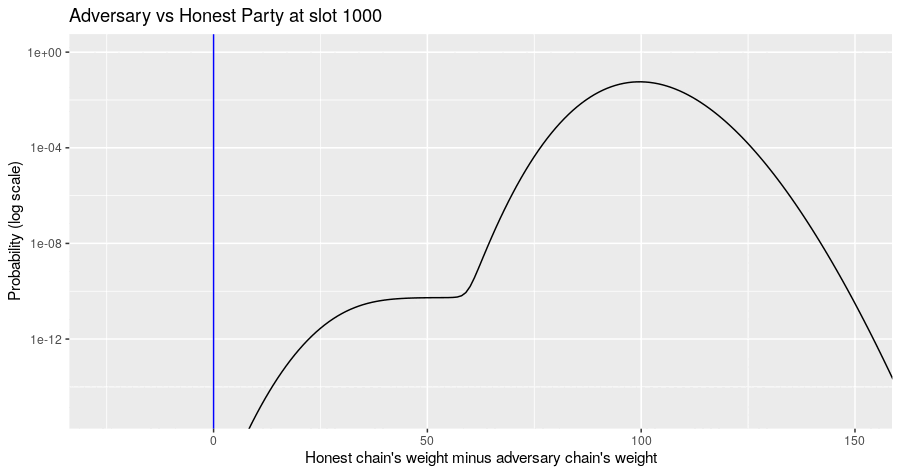
The Markov simulation results in a probability distribution of possible states of the block tree, given the adversary's strategy. The probability distribution of metrics of interest can be computed from that. For example, the diagram below shows the evolution of the probability distribution for the difference of the honest chain's weight minus the adversarial chain's weight for the situation where the adversary builds their chain privately and never assists the honest parties in forming a quorum. Note the jump in the distribution at multiples of slot 150, when there is a high probability that the honest party's chain gains a certificate.

Application of Praos margin and reach simulation to Peras

The article Practical Settlement Bounds for Longest-Chain Consensus by Gaži, Ren, and Russell, (2023) provides recurrence relations for margin and reach that can be solved numerically to determine the probability of settlement failure. The computations are relevant for Peras (i) after one block has been certified and before a subsequent block is certified and (ii) during the cool-down period. We used their software (see https://github.com/renling/LCanalysis) to repeat their computation and extend it to more blocks. This approach accounts for the diffusion time Δ, computes in terms of blocks instead of slots, does not make the two-chain (one honest and one adversarial) assumption, and is supported by mathematical rigor.

Analyses of adversarial scenarios

The probability of adversarial success can be computed analytically, either exactly or approximately, for some scenarios. Such analytic computations are typically faster and more comprehensive than running ensembles of simulations and analyzing those results. The scenarios analyzed in this section are intended to provide guidance on how the probability of adversarial success depends upon Peras parameters, so that the parameters can be set appropriately for stakeholder user cases. In this section we use the following notation:

• Active-slot coefficient: $\alpha$
• Round length: $U$
• Block-selection offset: $L$
• Certificate expiration: $A$
• Quorum for creating a certificate: $\tau = \frac{3}{4} n$
• Fraction of adversarial stake: $f$
• Mean size of the voting committee: $n$
• Per-slot probability of a block:
  • Honest block: $p = 1 - (1 - \alpha)^{1 - f} \approx \alpha \cdot (1 - f)$
  • Adversarial block: $q = 1 - (1 - \alpha)^f \approx \alpha \cdot f$
• Binomial distribution of $n$ trials each with probability $p$ :
  • Probability density function: $\mathbf{p}_\text{binom}(k,n,p)= {n\choose{k}} \cdot p^k \cdot (1 - p)^{n-k}$
  • Cumulative probability function: $\mathbf{P}_\text{binom}(m,n,p) = \sum_{k=0}^m \mathbf{p}(k,n,p)$
• Normal distribution with mean $\mu$ and standard deviation $\sigma$:
  • Probability density function: $\mathbf{p}_\text{normal}(x, \mu, \sigma) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{- \frac{(x - \mu)^2}{2 \sigma^2}}$
  • Cumulative probability function: $\mathbf{P}_\text{normal}(x,\mu,\sigma) = \int_{-\infty}^x dt \, \mathbf{p}_\text{normal}(t, \mu, \sigma)$

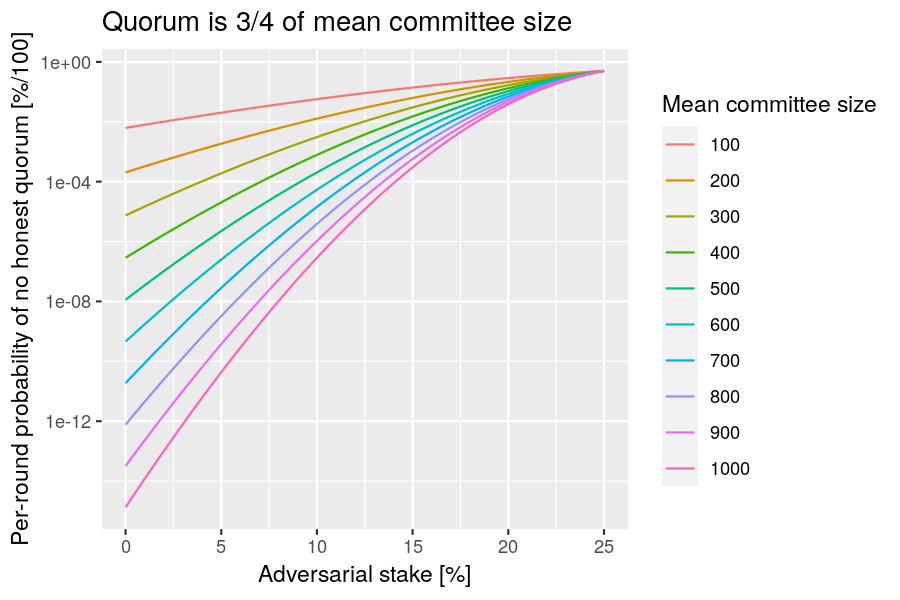
No honest quorum in round

Question: What is the probability of not reaching a quorum if adversaries abstain from voting?

Relevance: This analysis can be used to select a mean committee size that is appropriate for a given risk tolerance.

Risk: A adversary can trigger a cool-down period if they abstain from voting.

Scenario: Consider the situation where the adversary decides not to vote in a round, in order to prevent a quorum from occurring and to force the chain into a cool-down period. This occurs when the number of honest voters is less than the quorum size.

Analysis

Analysis: Let $\beta$ be the probability that a unit of stake is selected for voting-committee membership. Let $S$ be the total stake and $H = (1 - f) \cdot S$ be the honest stake. Assuming the total stake is large, we can approximate the binomial distribution by a normal one and express the probability of not having an an honest quorum as follows:

$$P = \mathbf{P}_\text{binom} (\lfloor\tau\rfloor, H, \beta) \approx \mathbf{P}_\text{normal} \left( \tau, H \cdot \beta, \sqrt{H \cdot \beta \cdot (1 - \beta)} \right) \approx \mathbf{P}_\text{normal} \left( \tau, H \cdot \beta, \sqrt{H \cdot \beta} \right)$$

Now set the quorum size to the recommended value $\tau = \frac{3}{4} n$ to discover a simple relationship:

$$P \approx \mathbf{P}_\text{normal} \left( f , \frac{1}{4} , \sqrt{\frac{1 - f}{n}} \right)$$

The following R function performs this computation:

function(f, n)
  pnorm(f, 1 / 4, sqrt((1 - f) / n))

Example: Plot the probability of not having an honest quorum as a function of the adversarial fraction of stake, for various mean sizes of the voting committee.

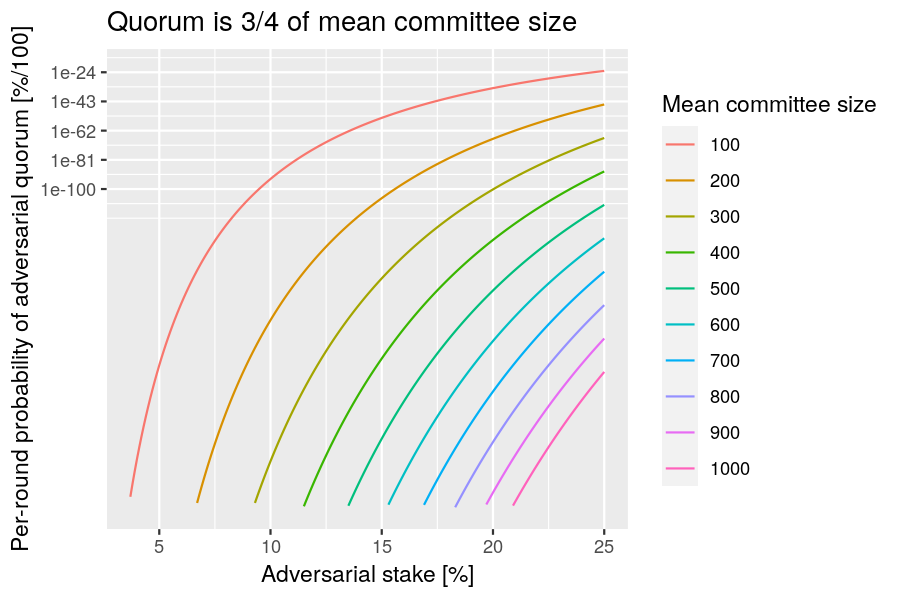
Adversarial quorum

Question: What is the probability that adversaries can form a voting quorum in a round?

Relevance: This analysis can be used to select a mean committee size that is appropriate for a given risk tolerance.

Risk: An adversary can boost an adversarial fork.

Scenario: Consider the situation where adversaries are lucky enough in the voting-committee sortition to hold a quorum of votes and create an "adversarial certificate".

Analysis

The analysis proceeds similarly to the "no honest quorum" scenario, but for adversaries having at least a quorum of votes.

$$P = 1 - \mathbf{P}_\text{binom} (\lceil\tau\rceil, S - H, \beta) \approx 1 - \mathbf{P}_\text{normal} \left( \tau, (S - H) \cdot \beta, \sqrt{(S - H) \cdot \beta \cdot (1 - \beta)} \right) \approx 1 - \mathbf{P}_\text{normal} \left( \tau, f \cdot n, \sqrt{f \cdot n} \right)$$

Now set the quorum size to the recommended value $\tau = \frac{3}{4} C$ to discover a simple relationship:

$$P \approx \mathbf{P}_\text{normal} \left( f , \frac{3}{4} , \sqrt{\frac{f}{n}} \right)$$

The following R function performs this computation:

function(f, n)
  pnorm(f, 3 / 4, sqrt(f / n))

Example: Plot the probability of having an adversarial quorum as a function of the adversarial fraction of stake, for various mean sizes of the voting committee.

No certificate in honest block

Question: What is the probability that adversaries can prevent a certificate from being included in a block before the certificate expires?

Relevance: This analysis can be used to set the certificate-expiration parameter $A$.

Risk: An adversary can trigger a premature ending of the cool-down period (via rule VR-2B) by preventing a new $\mathsf{cert}^*$ from being recorded in a block.

Scenario: Consider the situation where the voting certificate must be included on the chain (via protocol rule BC5), but no honest blocks are forged before the last $\mathsf{cert}^\prime$ expires and adversaries abstain from updating $\mathsf{cert}^\prime$ when they forge blocks.

Analysis

The probability that adversaries forge every block during the period when the certificate has not expired is

$$P = (1 - p)^A = (1 - \alpha)^{(1 - f) \cdot A}$$

and this can be represented as the following R function:

function(A, f, alpha)
  (1 - alpha)^((1 - f) * A)

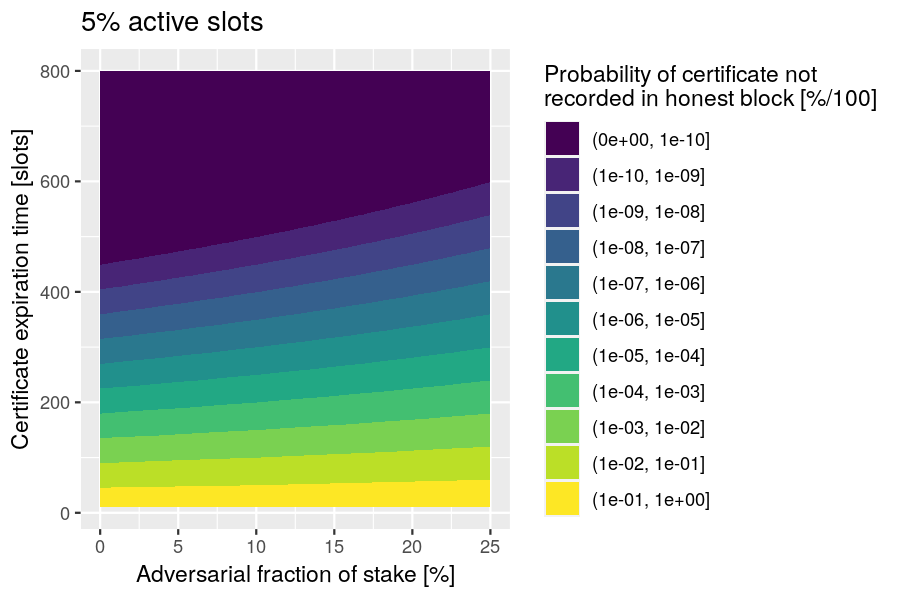
Example: Assuming an active-slot coefficient of 5%, plot the probability of a certificate not being recorded in an honest block before the certificate expires.

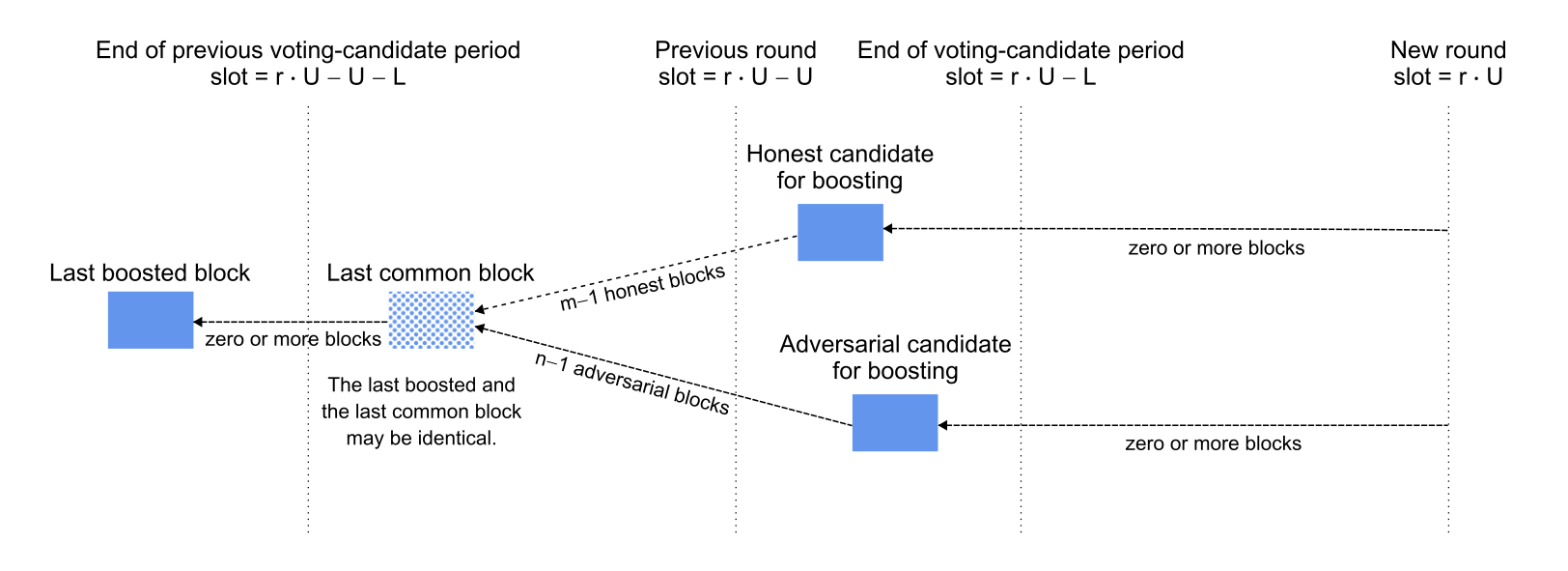
Adversarial chain receives boost

Here we examine two approaches to computing the probability that an adversarial chain receives a voting boost.

Variant 1

Question. What is the probability that an adversarial chain receives the next boost?

Relevance: This analysis provides guidance on selecting the round length.

Risk: An adversary can anchor their chain by having one of its later blocks boosted.

Scenario. It currently is round $r$ and a certificate was created in round $r - 1$ for a block at least $U + L$ slots in the past that is also in the common prefix of the honest and adversarial chains. The honest parties lengthen one fork by $m \ge 0$ blocks to the next candidate for voting (i.e., the newest block on that fork that is at least $L$ slots old) and the adversarial parties similarly lengthen a separate fork by $n \ge 0$ blocks. If the adversarial chain is revealed to the honest parties before the start of the new round $r$ and if the adversarial chain is longer (i.e., $n > m$), then the voting committee will vote to boost the adversarial chain. The per-slot probability of adding a block to the honest or adversarial chain is $p$ or $q$, respectively.

Analysis

Assume that the block- and vote-diffusion times are negligible, so that the last boosted block is indeed the last block before slot $r \cdot U - U - L$ and that the honest and adversarial candidates are indeed the last blocks on their forks before slot $r \cdot U - l$. (Note that this neglects the probability that the adversary will privately extend the last boosted block before slot $r \cdot U - U - L$.) Thus the lengthening of the two forks during the $U$ slots are the last boosted block are binomially distributed with parameters $m$ and $p$ (honest) and $n$ and $p$ (adversarial). The probability of $m < n$ is

$$P = \sum_{0 \le m < n \le U} \mathbf{p}_\text{binom}(m,U,p) \cdot \mathbf{p}_\text{binom}(n,U,q) = \sum_{n=1}^U \mathbf{P}_\text{binom}(n-1,U,p) \cdot \mathbf{p}_\text{binom}(n,U,q)$$

and the following R function implements this computation:

function(U, p, q)
  sum( pbinom(1:U-1, U, p) * dbinom(1:U, U, q) )

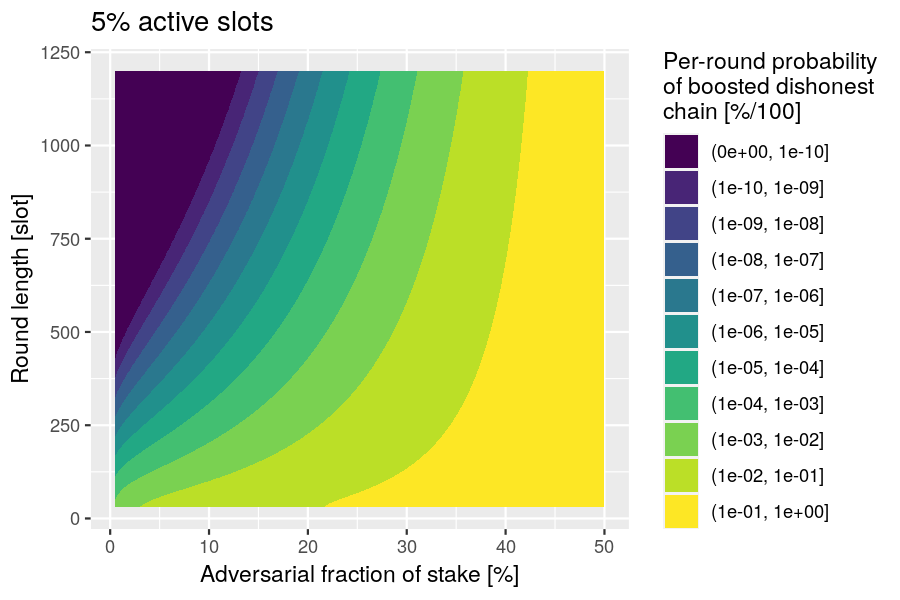
Example. Let the active-slot coefficient $\alpha = 0.05 \, \text{slot}^{-1}$ and let $f$ be the fraction of adversarial stake, so $p = \alpha \cdot (1 - f)$ and $q = \alpha \cdot f$. Plot the probability of the dishonest boost as a function of the adversarial fraction of stake and the round length.

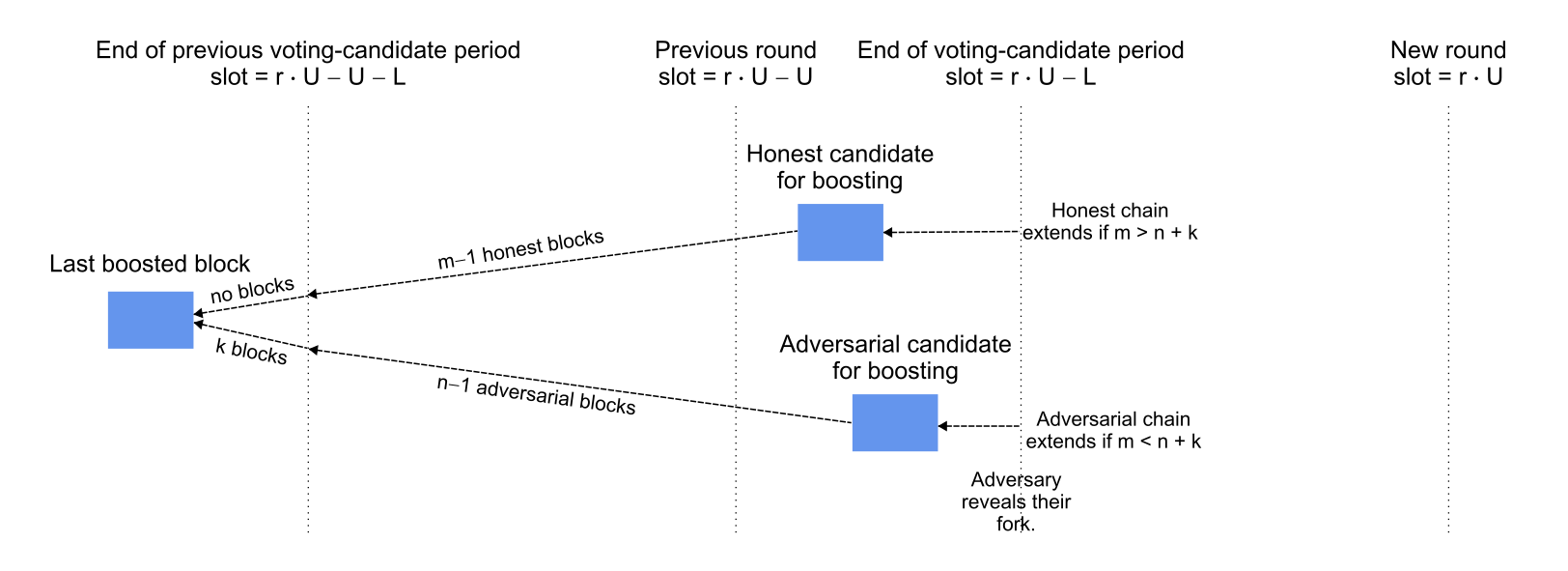
Variant 2

Question. What is the probability that an adversarial chain receives the next boost?

Relevance: This analysis provides guidance on selecting the round length.

Risk: An adversary can anchor their chain by having one of its later blocks boosted, resulting in honest blocks being rolled back.

Scenario. It currently is round $r$ and a certificate was created in round $r - 1$ for a block at least $U + L$ slots in the past that is also the common prefix of the honest and adversarial chains. The honest parties lengthen one fork by $m \ge 0$ blocks to the next candidate for voting (i.e., the newest block on that fork that is at least $L$ slots old) and the adversarial parties similarly lengthen a separate fork by $k \ge 0$ blocks before slot $r \cdot U - U - L$ and by $n \ge 0$ blocks subsequently. If the adversarial chain is revealed to the honest parties at slot $r \cdot U = L$ and if the adversarial chain is longer (i.e., $k + n > m$), then all parties will extend the adversarial chain and then next voting committee will boost the adversarial chain, causing the $m$ honest blocks to be rolled back.

Analysis

Assume that the block- and vote-diffusion times are negligible, so that the last boosted block is indeed the last public block before slot $r \cdot U - U - L$ and that the honest and adversarial candidates are indeed the last blocks on their forks before slot $r \cdot U - l$. Thus the lengthening of the two forks during the $U$ slots are the last boosted block are binomially distributed with parameters $m$ and $p$ (honest) and $n$ and $p$ (adversarial). Additionally, the adversary may privately produce $k$ blocks after the last boosted block and before slot $r \cdot U - U - L$: this random variable for producing such blocks is negative-binomially distributed. The probability of $m < k + n$ is

$$P = \sum_{\substack{0 \le m \le U \\ 0 \le n \le U \\ 0 \le k \le \infty \\ m < n + k}} (1 - f) f^k \cdot {U\choose{m}} p^m (1-p)^{U-m} \cdot {U\choose{n}} q^n (1-q)^{U-n}$$

which simplifies to

$$P = (1 - f) \cdot \sum_{n=1}^U \mathbf{P}_\text{binom}(n-1,U,p) \cdot \mathbf{p}_\text{binom}(n,U,q) + (1 - f) \cdot \sum_{k=1}^U f^k \cdot \sum_{n=0}^{U-k} \mathbf{P}_\text{binom}(n+k-1,U,p) \cdot \mathbf{p}_\text{binom}(n,U,q) + f^{U+1}$$

and we can be implemented in R as the following function:

function (U, p, q) {
  f <- q / (p + q)
  p0 <- (1 - f) * sum( pbinom(0:(U-1), U, p) * dbinom(1:U, U, q) )
  pk <- (1 - f) * sum( mapply(function(k) f^k * sum( pbinom((k-1):(U-1), U, p) * dbinom(0:(U-k), U, q) ), 1:U) )
  pinf <- f^(U+1)
  p0 + pk + pinf
}

Example. Let the active-slot coefficient $\alpha = 0.05 \, \text{slot}^{-1}$ and let $f$ be the fraction of adversarial stake, so $p = \alpha \cdot (1 - f)$ and $q = \alpha \cdot f$. Plot the probability of the dishonest boost as a function of the adversarial fraction of stake and the round length.

Healing from adversarial boost

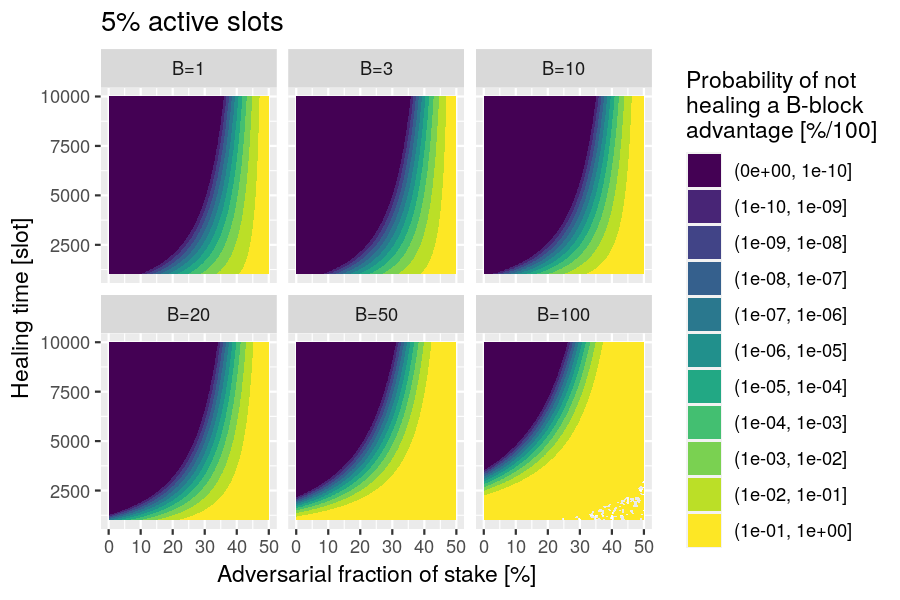
Question: How long does it take to neutralize the adversarial advantage of a certificate?

Relevance: "During the initial “healing” phase of the cooldown period, parties continue with standard Nakamoto block creation until the potential advantage of B that the adversary could gain with a certificate is neutralized." This healing time helps determine the value of the certificate-expiration time $A$ and the chain-ignorance period $R$.

Risk: An adversary can cause their fork to be preferred for an extended period if it has a certificate.

Scenario: The honest chain must grow at least $B$ blocks longer than the adversarial chain if it is to resist the adversarial chain's receiving a boost from a certificate.

Analysis

During cooldown, the growth of the honest chain (length $m$) and adversarial chain (length $n$) can be modeled by the difference between binomially distributed random variables. The probability of $m < n + B$ at slot $s$ is

$$P = \sum_{0 \le m < n + B \le s} \mathbf{p}_\text{binom}(m, s, p) \cdot \mathbf{p}_\text{binom}(n, s, q) = \sum_{n=0}^s \mathbf{P}_\text{binom}(n+B-1, s, p) \cdot \mathbf{p}_\text{binom}(n, s, q)$$

and can be computed by the following R function:

function(s, B, p, q)
  sum(pbinom((B-1):(s+B-1), s, p) * dbinom(0:s, s, q))

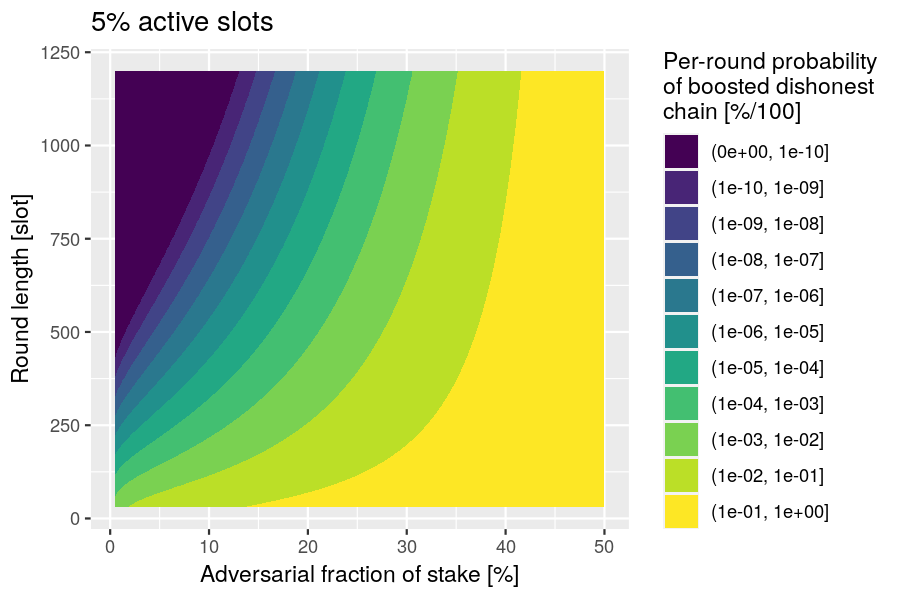
Example: Plot the probability of the honest chain not healing from an adversarial boost, as a function of the healing time $s$ and the boost $B$, under the assumption that the active-slot coefficient is $\alpha = 0.05 \, \text{slot}^{-1}$.

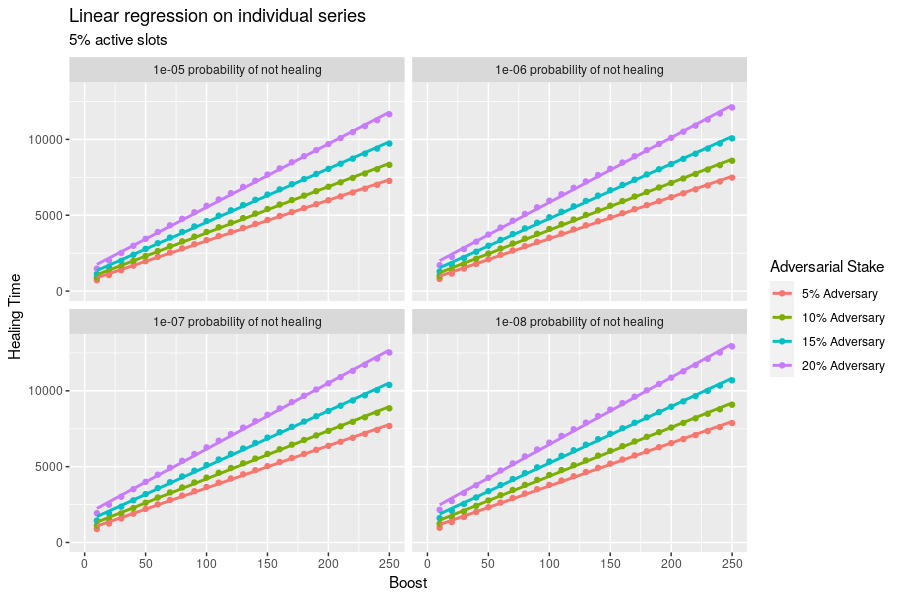
This healing time scales approximately linearly with the boost parameter. The diagram below shows the relationship between these two parameters along with a linear fit at different probabilities of not healing and different adversarial stakes.

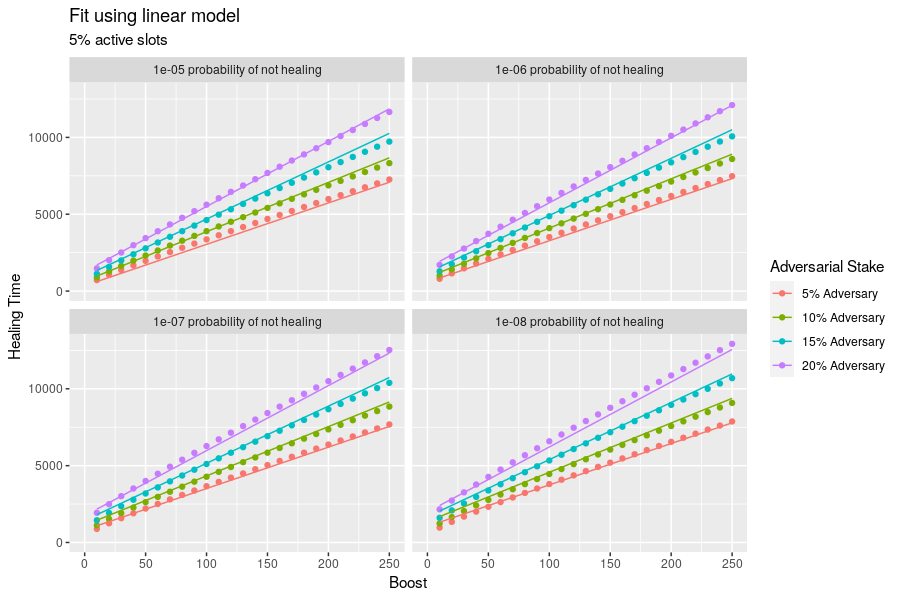
If we fit this dataset to a linear model, we find the following relationships and quality of fit. Note that this model is no suitable for use outside of the ranges of the training data: in particular, there is a much stronger dependence on boost for small probabilities and large adversarial stakes.

Call:
lm(formula = `Healing Time` ~ (`Boost` + `Adversarial Stake`)^2 + log(`Probability of Not Healing`))

Residuals:
    Min      1Q  Median      3Q     Max
-539.43 -141.38  -39.61  168.45  437.53

Coefficients:
                                    Estimate Std. Error t value Pr(>|t|)
(Intercept)                       -1142.2130    79.5507  -14.36   <2e-16 ***
`Boost`                              21.8229     0.3509   62.19   <2e-16 ***
`Adversarial Stake`                6200.4250   380.9661   16.28   <2e-16 ***
log(`Probability of Not Healing`)  -102.2989     4.0128  -25.49   <2e-16 ***
`Boost`:`Adversarial Stake`         102.4693     2.5627   39.99   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 206.6 on 395 degrees of freedom
Multiple R-squared:  0.9945,	Adjusted R-squared:  0.9945
F-statistic: 1.796e+04 on 4 and 395 DF,  p-value: < 2.2e-16

No honest block

Question: What is the probability of not having an honest block during a given period of time?

Relevance: "In the subsequent phase, parties are required to submit the latest certificate they are aware of to the chain." This chain-quality time helps determine the value of the certificate-expiration time $A$ and the chain-ignorance period $R$.

Risk: The registration of a certificate during cooldown might require waiting for an honest block where it can be included.

Scenario, Analysis, Example: The scenario, analysis, and example are identical to the case "No certificate in honest block".

No common prefix

Question: How long can an adversary maintain a common prefix?

Relevance: "Finally, in the third phase, parties wait until the blocks from the second phase have stabilized." This common-prefix time helps determine the value of the cooldown period $K$.

Risk: A strong adversary can keep their fork viable for many slots.

Scenario: The honest chain must grow longer than the adversarial chain.

Analysis

During cooldown, the growth of the honest chain (length $m$) and adversarial chain (length $n$) can be modeled by the difference between binomially distributed random variables. The probability of $m \le n$ at slot $s$ is

$$P = \sum_{0 \le m \le n \le s} \mathbf{p}_\text{binom}(m, s, p) \cdot \mathbf{p}_\text{binom}(n, s, q) = \sum_{n=0}^s \mathbf{P}_\text{binom}(n, s, p) \cdot \mathbf{p}_\text{binom}(n, s, q)$$

and can be computed by the following R function:

function(s, p, q)
  sum(pbinom(0:s, s, p) * dbinom(0:s, s, q))

Example: Plot the probability of the adversarial chain being at least as long as the honest chain, as a function of the common-prefix time $s$, under the assumption that the active-slot coefficient is $\alpha = 0.05 \, \text{slot}^{-1}$.

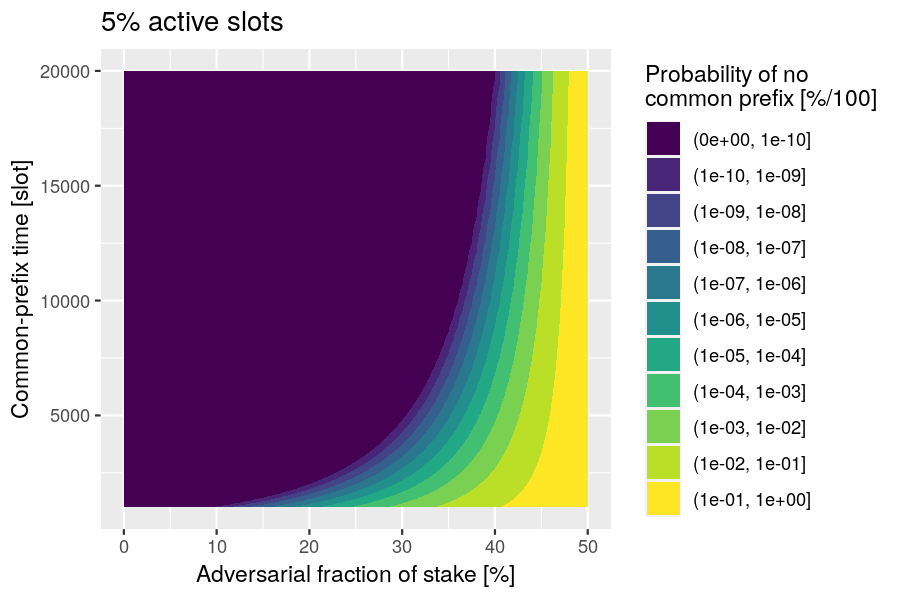
Defining Protocol Parameters values

In order to provide useful recommendations for the protocol parameters, we first need to understand what is their admissible range of values, e.g. the constraints stemming from practical and theoretical needs, and to analyse their impact on the settlement probabilities.

Constraints on Peras Parameters

The following constraints on Peras parameters arise for both theoretical and practical considerations.

Parameter	Symbol	Units	Description	Constraints	Rationale
Round length	$U$	slots	The duration of each voting round.	$U \geq \Delta$	All of a round's votes must be received before the end of the round.
Block selection offset	$L$	slots	The minimum age of a candidate block for being voted upon.	$\Delta < L \leq U$	Rule VR-1B will fail if the candidate block is older than the most recently certified block.
Certificate expiration	$A$	slots	The maximum age for a certificate to be included in a block.	$A = T_\text{heal}+T_\text{CQ}$	After a quorum failure, the chain must heal and achieve quality.
Chain ignorance period	$R$	rounds	The number of rounds for which to ignore certificates after entering a cool-down period.	$R = \left\lceil A / U \right\rceil$	Ensure chain-ignorance period lasts long enough to include a certificate on the chain.
Cool-down period	$K$	rounds	The minimum number of rounds to wait before voting again after a cool-down period starts.	$K = \left\lceil \frac{A + T_\text{CP}}{U} \right\rceil$	After a quorum failure, the chain must heal, achieve quality, and attain a common prefix.
Certification boost	$B$	blocks	The extra chain weight that a certificate gives to a block.	$B > 0$	Peras requires that some blocks be boosted.
Quorum size	$\tau$	parties	The number of votes required to create a certificate.	$\tau > 3 n / 4$	Guard against a minority (< 50%) of adversarial voters.
Committee size	$n$	parties	The number of members on the voting committee.	$n > 0$	Peras requires a voting committee.
Network diffusion time	$\Delta$	slots	Upper limit on the time needed to diffuse a message to all nodes.	$\Delta > 0$	Messages have a finite delay.
Active slot coefficient	$f$	1/slots	The probability that a party will be the slot leader for a particular slot.	$0 < f \leq 1$	Blocks must be produced.
Healing time	$T_\text{heal}$	slots	Healing period to mitigate a strong (25-50%) adversary.	$T_\text{heal} = \mathcal{O}\left( B / f \right)$	Sufficient blocks must be produced to overcome an adversarially boosted block.
Chain-quality time	$T_\text{CQ}$	slots	Ensure the presence of at least one honest block on the chain.	$T_\text{CQ} = \mathcal{O} (k/f)$	A least one honest block must be produced.
Common-prefix time	$T_\text{CP}$	slots	Achieve settlement.	$T_\text{CP} = \mathcal{O} (k/f)$	The Ouroboros Praos security parameter defines the time for having a common prefix.
Security parameter	$k$	blocks	The Ouroboros Praos security parameter.	n/a	Value for the Cardano mainnet.

Settlement probabilities

In the estimates below, we define the non-settlement probability as the probability that a transaction (or block) is rolled back. Note that this does not preclude the possibility that the transaction could be included in a later block because it remained in the memory pool of a node that produced a subsequent block. Because there are approximately 1.5 million blocks produced per year, even small probabilities of non-settlement can amount to an appreciable number of discarded blocks.

Case 1: Blocks without boosted descendants

Blocks that are not cemented by a boost to one of their descendant (successor) blocks are most at risk for being rolled back because they are not secured by the extra weight provided by a boost.

The Variant 2 scenario in the Adversarial chain receives boost section above dominates the situation where a transaction is recorded in a block but an adversarial fork later is boosted by a certificate to become the preferred chain. This scenario plays out as follows:

1. Both the honest chain and an initially private adversarial chain have a common prefix that follows the last boosted block.
2. The adversary privately grows their chain and does not include transactions in the memory pool.
3. When the time comes where the last block is first eligible for later being voted upon, the adversarial chain is published and all parties see that it is longer than the honest chain.
4. Hence the newly published adversarial chain becomes the preferred chain, and all parties build upon that.
5. Later, when voting occurs, the chain that had been adversarial will received the boost.
6. Because the adversarial prefix has been boosted, there is a negligible probability that the discarded portion of the honest chain will ever become part of the preferred chain.
7. Therefore the preferred chain does not include any transactions that were in blocks of the honest chain after the common prefix and before the adversarially boosted block.

Note that this is different from the situation where a transaction is included on honest forks because such a transaction typically reaches the memory pool of the block producers on each fork and is included on each. The adversary refrains from including the transaction on their private chain.

The active-slot coefficient (assumed to be 5%), the length of the rounds, and the adversary's fraction of stake determine the probability of non-settlement in such a scenario. The table below estimates this probability. For example, in the presence of a 5% adversary and a round length of 360 slots, one could expect about two blocks to be reverted per year in such an attack.

Round Length	5% Adversary	10% Adversary	15% Adversary	20% Adversary	45% Adversary
60	1.35e-02	3.64e-02	6.99e-02	1.15e-01	4.81e-01
90	5.45e-03	1.82e-02	4.14e-02	7.77e-02	4.64e-01
120	2.16e-03	9.16e-03	2.47e-02	5.31e-02	4.48e-01
150	8.55e-04	4.63e-03	1.49e-02	3.66e-02	4.34e-01
180	3.40e-04	2.36e-03	9.08e-03	2.55e-02	4.22e-01
240	5.46e-05	6.27e-04	3.42e-03	1.25e-02	4.00e-01
300	8.91e-06	1.69e-04	1.31e-03	6.27e-03	3.81e-01
360	1.47e-06	4.63e-05	5.11e-04	3.18e-03	3.65e-01
420	2.46e-07	1.28e-05	2.00e-04	1.63e-03	3.51e-01
480	4.12e-08	3.56e-06	7.92e-05	8.37e-04	3.37e-01
540	6.97e-09	9.96e-07	3.15e-05	4.33e-04	3.25e-01
600	1.18e-09	2.80e-07	1.26e-05	2.25e-04	3.14e-01

Using the approach of Gaži, Ren, and Russell (2023) and setting $\Delta = 5 \text{\,slots}$ to compute the upper bound on the probability of failure to settle results in similar, but not identical probabilities.

Blocks	≈ Slots	5% Adversary	10% Adversary	15% Adversary	20% Adversary
3	60	6.13e-02	1.41e-01	2.53e-01	3.89e-01
4	80	2.73e-02	8.15e-02	1.73e-01	3.01e-01
5	100	1.22e-02	4.73e-02	1.19e-01	2.34e-01
6	120	5.46e-03	2.75e-02	8.26e-02	1.83e-01
9	180	4.95e-04	5.55e-03	2.80e-02	8.89e-02
12	240	4.51e-05	1.13e-03	9.65e-03	4.40e-02
15	300	4.11e-06	2.32e-04	3.35e-03	2.20e-02
18	360	3.75e-07	4.77e-05	1.17e-03	1.11e-02
21	420	3.42e-08	9.83e-06	4.11e-04	5.60e-03
24	480	3.13e-09	2.03e-06	1.44e-04	2.83e-03
27	540	2.85e-10	4.17e-07	5.06e-05	1.44e-03
30	600	2.60e-11	8.60e-08	1.78e-05	7.30e-04

Case 2: Blocks with boosted descendants

Once one of a block's descendants (successors) has been boosted by a certificate, it is much more difficult for an adversary to cause it to be rolled back because they adversary must overcome both count of blocks on the preferred, honest chain and the boost that chain has already received.

The Healing from adversarial boost section above provides the machinery for estimating the probability of an adversary building a private fork that has more weight than a preferred, honest chain that has been boosted. The scenario plays out as follows:

1. Both the honest chain and an initially private adversarial chain have a common prefix that precedes the last boosted block.
2. The adversary privately grows their chain.
3. When the adversary's chain is becomes long enough to overcome both the honest blocks and the boost, the adversarial chain is published and all parties see that it is longer than the honest chain.
4. Hence the newly published adversarial chain becomes the preferred chain, and all parties build upon that.
5. Therefore the preferred chain does not include any transactions that were in blocks of the honest chain after the common prefix.

Typically, the adversary would only have a round's length of slots to build sufficient blocks to overcome the boosted, honest, preferred fork. After that, the preferred fork would typically receive another boost, making it even more difficult for the adversary to overcome it. The table below shows the probability that of non-settlement for a block after the common prefix but not after the subsequent boosted block on the honest chain, given a 5% active slot coefficient and a 5 blocks/certificate boost.

Round Length	5% Adversary	10% Adversary	15% Adversary	20% Adversary	45% Adversary
60	3.09e-08	1.08e-06	8.94e-06	4.07e-05	3.10e-03
90	5.91e-08	2.27e-06	2.03e-05	9.91e-05	9.36e-03
120	6.32e-08	2.73e-06	2.70e-05	1.44e-04	1.74e-02
150	5.01e-08	2.49e-06	2.77e-05	1.62e-04	2.57e-02
180	3.31e-08	1.94e-06	2.45e-05	1.59e-04	3.37e-02
240	1.07e-08	8.98e-07	1.51e-05	1.23e-04	4.74e-02
300	2.73e-09	3.44e-07	7.88e-06	8.19e-05	5.80e-02
360	6.15e-10	1.20e-07	3.78e-06	5.04e-05	6.62e-02
420	1.29e-10	3.94e-08	1.73e-06	2.96e-05	7.23e-02
480	2.57e-11	1.25e-08	7.65e-07	1.70e-05	7.70e-02
540	4.98e-12	3.88e-09	3.33e-07	9.56e-06	8.05e-02
600	9.43e-13	1.19e-09	1.43e-07	5.32e-06	8.31e-02

A boost of 10 blocks/certificate makes the successful adversarial behavior even less likely.

Round Length	5% Adversary	10% Adversary	15% Adversary	20% Adversary	45% Adversary
60	< 1e-16	4.92e-14	2.98e-12	5.56e-11	2.23e-07
90	7.77e-16	8.89e-13	5.65e-11	1.10e-09	4.98e-06
120	3.55e-15	4.47e-12	3.01e-10	6.15e-09	3.27e-05
150	8.88e-15	1.16e-11	8.39e-10	1.82e-08	1.16e-04
180	1.38e-14	2.01e-11	1.59e-09	3.70e-08	2.90e-04
240	1.60e-14	2.97e-11	2.87e-09	7.93e-08	9.83e-04
300	1.05e-14	2.53e-11	3.08e-09	1.03e-07	2.13e-03
360	4.77e-15	1.57e-11	2.48e-09	1.02e-07	3.62e-03
420	1.55e-15	7.98e-12	1.67e-09	8.59e-08	5.31e-03
480	4.44e-16	3.56e-12	9.96e-10	6.46e-08	7.08e-03
540	4.44e-16	1.45e-12	5.49e-10	4.52e-08	8.85e-03
600	2.22e-16	5.54e-13	2.86e-10	3.00e-08	1.06e-02

A boost of 15 blocks/certificate makes the successful adversarial behavior even less likely.

Round Length	5% Adversary	10% Adversary	15% Adversary	20% Adversary	45% Adversary
60	< 1e-16	< 1e-16	< 1e-16	< 1e-16	9.81e-13
90	< 1e-16	< 1e-16	2.22e-16	8.88e-16	2.24e-10
120	< 1e-16	< 1e-16	2.22e-16	2.39e-14	6.59e-09
150	1.11e-16	1.11e-16	2.78e-15	2.19e-13	6.90e-08
180	< 1e-16	2.22e-16	1.18e-14	1.07e-12	3.91e-07
240	< 1e-16	3.33e-16	7.89e-14	8.19e-12	4.29e-06
300	3.33e-16	4.44e-16	2.16e-13	2.61e-11	2.07e-05
360	1.11e-16	5.55e-16	3.49e-13	5.01e-11	6.26e-05
420	< 1e-16	6.66e-16	4.01e-13	6.97e-11	1.42e-04
480	< 1e-16	2.22e-16	3.68e-13	7.81e-11	2.65e-04
540	3.33e-16	2.22e-16	2.88e-13	7.53e-11	4.35e-04
600	2.22e-16	3.33e-16	2.00e-13	6.51e-11	6.47e-04

Recommendations for Peras parameters

Based on the analysis of adversarial scenarios, a reasonable set of default protocol parameters for further study and simulation is show in the table below. The optimal values for a real-life blockchain would depend strongly upon external requirements such as balancing settlement time against resisting adversarial behavior at high values of adversarial stake. This set of parameters is focused on the use case of knowing soon whether a block is settled or rolled back; other sets of parameters would be optimal for use cases that reduce the probability of roll-back at the expense of waiting longer for settlement.

Parameter	Symbol	Units	Value	Rationale
Round length	$U$	slots	90	Settlement/non-settlement in under two minutes.
Block-selection offset	$L$	slots	30	Several multiples of $\Delta$ to ensure block diffusion.
Certification boost	$B$	blocks	15	Negligible probability to roll back boosted block.
Security parameter	$k_\text{peras}$	blocks	3150	Determined by the Praos security parameter and the boost.
Certificate expiration	$A$	slots	27000	Determined by the Praos security parameter and boost.
Chain-ignorance period	$R$	rounds	300	Determined by the Praos security parameter, round length, and boost.
Cool-down period	$K$	rounds	780	Determined by the Praos security parameter, round length and boost.
Committee size	$n$	parties	900	1 ppm probability of no honest quorum at 10% adversarial stake.
Quorum size	$\tau$	parties	675	Three-quarters of committee size.

A block-selection offset of $L = 30 \text{\,slots}$ allows plenty of time for blocks to diffuse to voters before a vote occurs. Combining this with a round length of $U = 90 \text{\, slots}$ ensures that there is certainty in $U + L = 120 \text{\,slots}$ as to whether a block has been cemented onto the preferred chain by the presence of a certificate for a subsequent block. That certainty of not rolling back certified blocks is provided by a certification boost of $B = 15 \text{\,blocks}$ because of the infinitesimal probability of forging that many blocks on a non-preferred fork within the time $U$. Thus, anyone seeing a transaction appearing in a block need wait no more than two minutes to be certain whether the transaction is on the preferred chain (effectively permanently, less than a one in a trillion probability even at 45% adversarial stake) versus having been discarded because of a roll back. Unless the transaction has a stringent time-to-live (TTL) constraint, it can be resubmitted in the first $U - L = 60 \text{\,slots}$ of the current round, or in a subsequent round.

[!WARNING] The security-related computations in the next paragraph are not rigorous with respect to the healing, chain-quality, and common-prefix times, so they need correction after the research team reviews them and proposes a better approach.

The Praos security parameter $k_\text{praos} = 2160 \text{\,blocks} \approx 43200 \text{\,slots} = 12 \text{\,hours}$ implies a ~17% probability of a longer private adversarial chain at 49% adversarial stake. At that same probability, having to overcome a $B = 15 \text{\,blocks}$ adversarial boost would require $k_\text{peras} \approx 70200 \text{\,slots} = 3510 \text{\,blocks} = 19.5 \text{\,hours}$. This determines the certificate-expiration time as $A = k_\text{peras} - k_\text{praos} = 27000 \text{\,slots}$, the chain-ignorance period as $R = \left\lceil A / U \right\rceil = 300 \text{\,rounds}$, and the cool-down period as $K = \left\lceil k_\text{peras} / U \right\rceil = 780 \text{\,rounds}$.

The committee size of $n = 900 \text{\,parties}$ corresponds to a one in a million chance of not reaching a quorum if 10% of the parties do not vote for the majority block (either because they are adversarial, offline, didn't receive the block, or chose to vote for a block on a non-preferred fork). This "no quorum" probability is equivalent to one missed quorum in every 1.2 years. The quorum size of $\tau = \left\lceil 3 n / 4 \right\rceil = 675 \text{\,parties}$ is computed from this.

Protocol Formalisation

Formal specification in Agda

The formal specification of Ouroboros Peras is implemented in Agda as a relational specification. It provides a small-step semantics of the protocol that describes how the system can evolve over time.

Computational aspects in general are not considered and in many cases even left abstract. We make use of parameterization of modules to refer to those entities. The block-tree is an example of such a type that is not implemented in the formal specification, but on the other hand defined by properties specifying the behavior of an implementation of this data structure.

This is a different approach to the formal ledger specification, where the formal specification is also executable.

We considered the following approaches to link the formal specification with an executable specification in Haskell

• Decidable, relational specification in Agda: This would yield an executable specification, that can also be used in Haskell via the MAlonzo backend. Unfortunately agda2hs can not be used for code extraction, as the formal specification relies on the Agda standard library which is not supported by agda2hs

• Relational specification together with an executable test specification: The test specification can be lifted from Haskell into Agda and proven sound with respect to the formal specification in Agda. This approach does not provide us with a full executable specification, but this is also not required and just focusing on the properties to be executed in the test-cases is sufficient. In order to extract Haskell code only the lifted test specification is exported to Haskell using agda2hs and not the full small step semantics. For this step, we make use of Decidables from the agda2hs Prelude, as those, when extracted, drop the proof terms and evaluate to booleans.

The second approach has been chosen and implemented, see Conformance testing below.

In order for the formal specification to also establish a link with research, we started prototyping properties and proofs needed to show safety and liveness for Ouroboros Peras protocol. Those first attempts look promising and could potentially replace pen and paper proofs.

Note that as a minor restriction of the formal specification, we only model a fixed set of participants.

Conformance testing

Conformance testing is linked to the Peras specification via the following chain of evidence:

• The protocol is encoded in Agda as a relational specification.
• The proofs of Peras properties are written in Agda too.
• The protocol is also implemented as an executable specification in Agda.
• Soundness proofs demonstrate that the executable specification correctly implements the relational specification.
• The agda2hs tool generates Haskell code implementing the Agda executable specification.
• That Haskell code is used as the state model in the quickcheck-dynamic state-machine, property-based-testing framework.
• The implementation being tested is used as the run model.
• The quickcheck-dynamic tool generates arbitrary test cases and verifies that the run model obeys the properties of the state model.

The following types in the Agda executable specification are exported to Haskell.

record NodeModel : Set where
  field
    clock        : SlotNumber
    protocol     : PerasParams
    allChains    : List Chain
    allVotes     : List Vote
    allSeenCerts : List Certificate

data EnvAction : Set where
  Tick     : EnvAction
  NewChain : Chain → EnvAction
  NewVote  : Vote → EnvAction

initialModelState : NodeModel

transition : NodeModel → EnvAction → Maybe (List Vote × NodeModel)

This is used in the Haskell state model as follows.

instance StateModel NodeModel where
  data Action NodeModel a where
    Step :: EnvAction -> Action NodeModel [Vote]
  initialState = initialModelState
  precondition s (Step a) = isJust (transition s a)
  nextState s (Step a) _ = snd . fromJust $ transition s a

The present implementation focuses on the voting behavior, not on the block-production and network-diffusion behavior. For demonstration purposes, the RunModel is the Peras prototype/reference simulation describe in an earlier section of this document. Other implementations can be wired into the conformance tests via inter-process communication techniques.

$ peras-simulation-test --match "/Peras.Conformance.Test/" --qc-max-success=1000

Peras.Conformance.Test
  Prototype node
    Simulation respects model [✔]
      +++ OK, passed 1000 tests.

      Action polarity (50500 in total):
      100.000% +

      Actions (50500 in total):
      38.487% +NewVote
      30.816% +Tick
      30.697% +NewChain

Finished in 4.7193 seconds
1 example, 0 failures

Lessons learned from experiments with Agda-to-Haskell workflows

Aside from the workflow that we finally settled upon and that is described above, we explored several workflows for connecting the relational specification in Agda to quickcheck-dynamic tests in Haskell. This involves accommodating or working around several tensions:

• The relational specification uses the Agda Standard Library, which is not compatible with agda2hs.
  • Many of the Agda function names containing unicode characters or name patterns are not valid Haskell identifiers.
  • The MAlonzo representation of primitive types such as Maybe or tuples differs from the agda2hs representation of them in Haskell.
  • Type erasure via @0 in Agda can remove non-essential portions of an Agda type that depend upon the standard library.
  • The use of any non-compatible identifiers or types in the arguments or implementation of an Agda function prevents its use in Haskell.
  • Module parameters appear in the export of functions made by agda2hs.
• The MAlonzo code generated by Agda's GHC backend contains mangled names, making it difficult to call from Haskell.
  • The {-# COMPILE GHC ... as ... #-} pragmas are not comprehensive enough to deeply rename Agda constructs for use in Haskell.
  • Judicious use of the FOREIGN and COMPILE pragmas for both the GHC and AGDA2HS backends can achieve a seamlessness that avoids ever having to deal with mangled names. The basic strategy is to use Agda to define types that can be exported to Haskell, but then to import those back into Agda for its use in MAlonzo.
    • The data types used by Haskell clients must be created use Haskell.Prelude and be created by agda2hs via the {-# COMPILE AGDA2HS ... #-} pragma.
      • Types involving natural numbers must be hand-coded using {-# FOREIGN AGDA2HS ... #-} because they compile to Integer in MAlonzo but to Natural in agda2hs.
      • Fields may not contain identifiers that violate Haskell naming requirements.
    • Those types are used as the concrete implementation in the very module where they are defined via the {-# COMPILE GHC ... = data ... #-} pragma.
    • Functions that are called by Haskell are annotated with the {-# COMPILE GHC ... as ... #-} pragma.
      • Every argument must be of a type that was generated with {-# COMPILE AGDA2HS #-} or is a basic numeric type or unit.
      • Functions cannot have arguments using natural numbers, tuples, Maybe etc.
      • Functions may contain identifiers that violate Haskell naming requirements.
    • The agda --compile --ghc-dont-call-ghc --no-main command generates mangled Haskell under MAlonzo.Code.Peras, except that is uses the unmangled types in Peras and has unmangled function names.
• The situation would be far simplier if one could use a pure Agda state-machine testing framework instead of having to export code to Haskell and then test there.
• The StateModel and RunModel of quickcheck-dynamic seem a little out of sync with this use case where the model and its properties are known to be correct because of Agda proofs and only the implementation is being tested.

The following picture attempts to clarify the relationship between Agda and Haskell as it has been explored in a hybrid Agda/Haskell specification/testing implementation:

• Agda code relies on the Agda Standard Library which provide much better support for proofs than agda2hs and Haskell's Prelude obviously.
• Therefore Haskell code needs to depend on this stdlib code which is problematic for standard types (e.g., numbers, lists, tuples, etc.).
• The Agda code separates Types from Implementation in order to ease generation.
• Types are generated using agda2hs to provide unmangled names and simple structures on the Haskell side.
• Impl is generate usign GHC to enable full use of stdlib stuff, with toplevel interface functions generated with unmangled names.
• Types are also taken into account when compiling using GHC but they are only "virtual", namely the compiler makes the GHC-generated code depend on the agda2hs generated types.
• Hand-written Haskell code can call unmangled types and functions.

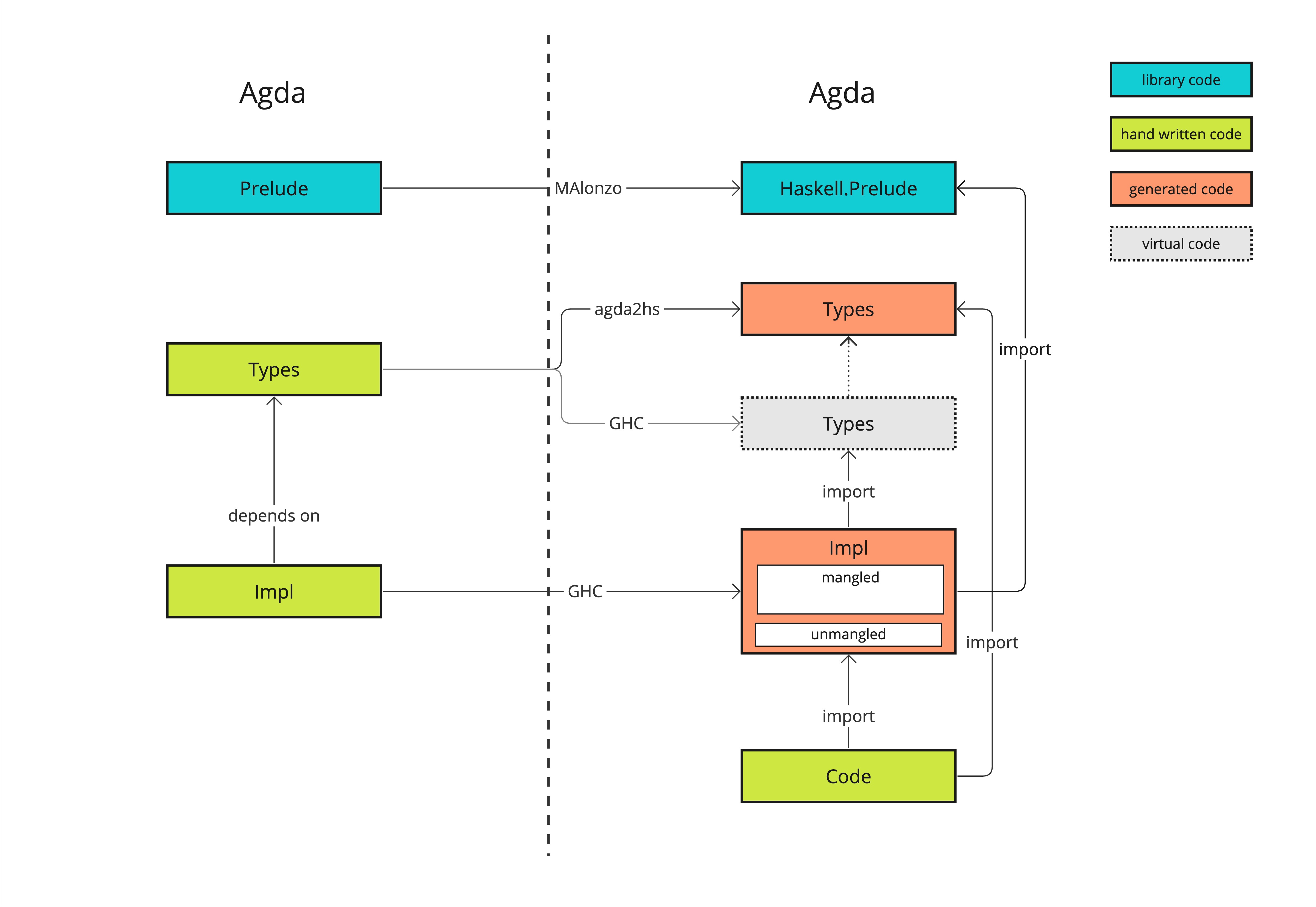
We used agda to generate MAlonzo-style Haskell code for the experimental Peras executable specification, Peras.QCD.Node.Specification. A quickcheck-dynamic test compares the MAlonzo version against the agda2hs version: these tests all pass, but the MAlonzo version runs significantly slower, likely because it involves more than two hundred Haskell modules.

• agda2hs version: 4m 45.206s (250 tests)
• MAlonzo version: 10m 46.280s (250 tests)

We also experimented with create a small embedded monadic DSL for writing the Peras specification in Agda in a manner so that it reads as pseudo-code understandable by non-Agda and non-Haskell programmers. For example, the executable specification for fetching looks like the following in this eDSL:

-- Enter a new slot and record the new chains and votes received.
fetching : List Chain → List Vote → NodeOperation
fetching newChains newVotes =
  do
    -- Increment the slot number.
    currentSlot ≕ addOne
    -- Update the round number.
    u ← peras U
    now ← use currentSlot
    currentRound ≔ divideNat now u
    -- Add any new chains and certificates.
    updateChains newChains
    -- Add new votes.
    votes ≕ insertVotes newVotes
    -- Turn any new quorums into certificates.
    newCerts ← certificatesForNewQuorums
    certs ≕ insertCerts newCerts
    -- Make the heaviest chain the preferred one.
    boost ← peras B
    heaviest ← heaviestChain boost <$> use certs <*> use chains
    preferredChain ≔ heaviest
    -- Record the latest certificate seen.
    updateLatestCertSeen
    -- Record the latest certificate on the preferred chain.
    updateLatestCertOnChain
    -- No messages need to be diffused.
    diffuse

There are still opportunities for syntactic sugar that would make the code more readable, but dramatic improvements probably are not feasible in this approach. Perhaps a more readable approach would be to express this in a rigorously defined, standardized pseudo-code language, which could be compiled to Agda, Haskell, Rust, Go, etc. Other lessons learned follow:

• Lenses improve readability.
• Using a List for the "set" data structure of the paper creates inefficiencies in the implementation.
  • Set invariants are not trivially enforced.
  • Access and query functions are slow.
• It might be difficult prove this executable specification matches the properties that are being formally proved.
• Even though the Agda code is written to look imperative, it has quite a few artifacts of functional style that could be an impediment to some implementors.
  • It might be better to use let statements instead of ← pure $. Unfortunately, it would be quite difficult to design an assignment operator to replace monadic let in Agda.
  • The functional style avoids introducing lots of intermediate variables, but maybe that would be preferable to using functions as modifiers to monadic state (e.g., _≕_ : Lens' s a → (a → a) → State s ⊤).
  • The use and pure functions could be eliminated by defining operators (including logical and arithmetic ones) that hide them.
• Overall, the Agda code is more verbose than the textual specification.
• It might be difficult to create Agda code that is simultaneously easily readable by mathematical audiences (e.g., researchers) and software audiences (e.g., implementors).
• Quite a bit of boilerplate (instances, helper functions, lenses, State monad, etc.) are required to make the specification executable.
• Creating a full eDSL might be a better approach, but that would involved significantly more effort.

Implementing Peras

Community feedback

As we want to turn Peras from a research idea into a concrete protocol extension, we want to provide to implementors the best possible tools to help them. We have therefore reached out to various people from the Cardano community asking them what would a good CIP for Peras look like.

• Varied Needs: Stakeholders have varying levels of technical expertise. Some require rigorous specifications (Agda, research papers), while others prefer high-level explanations and practical resources like pseudocode, diagrams, and data structure descriptions.
• Accessibility: There is a strong preference for CIPs (Cardano Improvement Proposals) to be understandable to a wider and diverse audience. dApp builders want to know if and what changes are required from them - i.e., how many confirmations they have to wait for before they can display to the user that the action is confirmed, SPOs want to know how much extra resources are neede and what effort is required for installation, etc.
• Transparency and Rationale: Stakeholders want clarity on the cost of Peras (in terms of ADA, fees, or resources) and a clear explanation of why this solution is possible now when it wasn't before.
• Speed and Efficiency: Some stakeholders emphasize the need for a faster development process, suggesting that the formal specification could be developed in parallel with the technical implementation.
• Timeline: Stakeholders are curious about the timeline for Peras development and implementation.

Resources impact of Peras

In this section, we evaluate the impact on the day-to-day operations of the Cardano network and cardano nodes of the deployment of Peras protocol, based on the data gathered over the course of project.

Network

Network traffic

For a fully synced nodes, the impact of Peras on network traffic is modest:

• For votes, assuming $U \approx 100$, a committee size of 2000 SPOs, a single vote size of 700 bytes, means we will be adding an average of 14 kB/s to the expected traffic to each node,
• For certificates, assuming an average of 50 kB size (half way between Mithril and ALBA sizes) means an negligible increase of 0.5 kB/s on average. Note that a node will download either votes or certificate for a given round, but never both so these numbers are not cumulative.

A non fully synced nodes will have to catch-up with the tip of the chain and therefore download all relevant blocks and certificates. At 50% load (current monthly load is 34% as of this writing), the chain produces a 45 kB block every 20 s on average. Here are back-of-the-napkin estimates of the amount of data a node would have to download (and store) for synchronizing, depending on how long it has been offline:

Time offline	Blocks (GB)	Certificates (GB)
1 month	5.56	1.23
3 months	16.68	3.69
6 months	33.36	7.38

Network costs

We did some research on network pricing for a few major Cloud and well-known VPS providers, based on the share of stakes each provider is reported to support, and some typical traffic pattern as exemplified by the following picture (courtesy of Markus Gufler).

The next table compares the cost (in US$/month) for different outgoing data transfer volumes expressed as bytes/seconds, on similar VMs tailored to cardano-node's hardware requirements (32GB RAM, 4+ Cores, 500GB+ SSD disk). The base cost of the VM is added to the network cost to yield total costs depending on transfer rate.

Provider	VM	50 kB/s	125 kB/s	250 kB/s
DigitalOcean	$188	$188	$188	$188
Google Cloud	$200	$213.6	$234	$268
AWS	$150 ?	$161.1	$177.9	$205.8
Azure	$175	$186	$202	$230
OVH	$70	$70	$70	$70
Hetzner	$32	$32	$32	$32

note

• The AWS cost is quite hard to estimate up-front, obviously on purpose. The $150 base price is a rough average of various instances options in the target range.
• Google, AWS and Azure prices are based on 100% uptime and at least 1-year reservation for discounts.
• Cloud providers only charge outgoing network traffic. The actual cost per GB depends on the destination, this table assumes all outbound traffic will be targeted outside of the provider which obviously won't be true, so it should be treated as an upper bound.

For an AWS hosted SPO, which represent about 20% of the SPOs, a 14 kB/s increase in traffic would lead to a cost increase of $3.8/mo (34 GB times $0.11/GB). This represents an average across the whole network: depending on the source of the vote and its diffusion pattern, some nodes might need to send a vote to more than one downstream peer which will increase their traffic, while other nodes might end up not needing to send a single vote to their own peers. Any single node in the network is expected to download each vote at most once.

Persistent storage

Under similar assumptions, we can estimate the storage requirements entailed by Peras: Ignoring the impact of cooldown periods, which last for a period at least as long as $k$ blocks, the requirement to store certificates for every round increases node's storage by about 20%.

Votes are expected to be kept in memory so their impact on storage will be null.

CPU

In the Votes & Certificates section we've provided some models and benchmarks for votes generation, votes verification, certificates proving and certificates verification, and votes diffusion. Those benchmarks are based on efficient sortition-based voting and ALBAs certificate, and demonstrate the impact of Peras on computational resources for a node will be minimal. Moreover, the most recent version of the algorithm detailed in this report is designed in such a way the voting process runs in parallel with block production and diffusion and therefore is not on this critical path.

Memory

A node is expected to need to keep in memory:

• Votes for the latest voting round: For a committee size of 1000 and individual vote size of 700 bytes, that's 700 kB.
• Cached certificates for voting rounds up to settlement depth, for fast delivery to downstream nodes: With a boost of 10/certificate, settlement depth would be in the order of 216 blocks, or 4320 seconds, which represent about 10 rounds of 400 slots. Each certificate weighing 50 kB, that's another 500 kB of data a node would need to cache in memory.

Peras should not have any significant impact on the memory requirements of a node.

Integration into Cardano Node

In the previous report, we already studied how Peras could be concretely implemented in a Cardano node. Most of the comments there are still valid, and we only provide here corrections and additions when needed. We have addressed resources-related issue in a previous section.

The following picture summarizes a possible architecture for Peras highlighting its interactions with other components of the system.

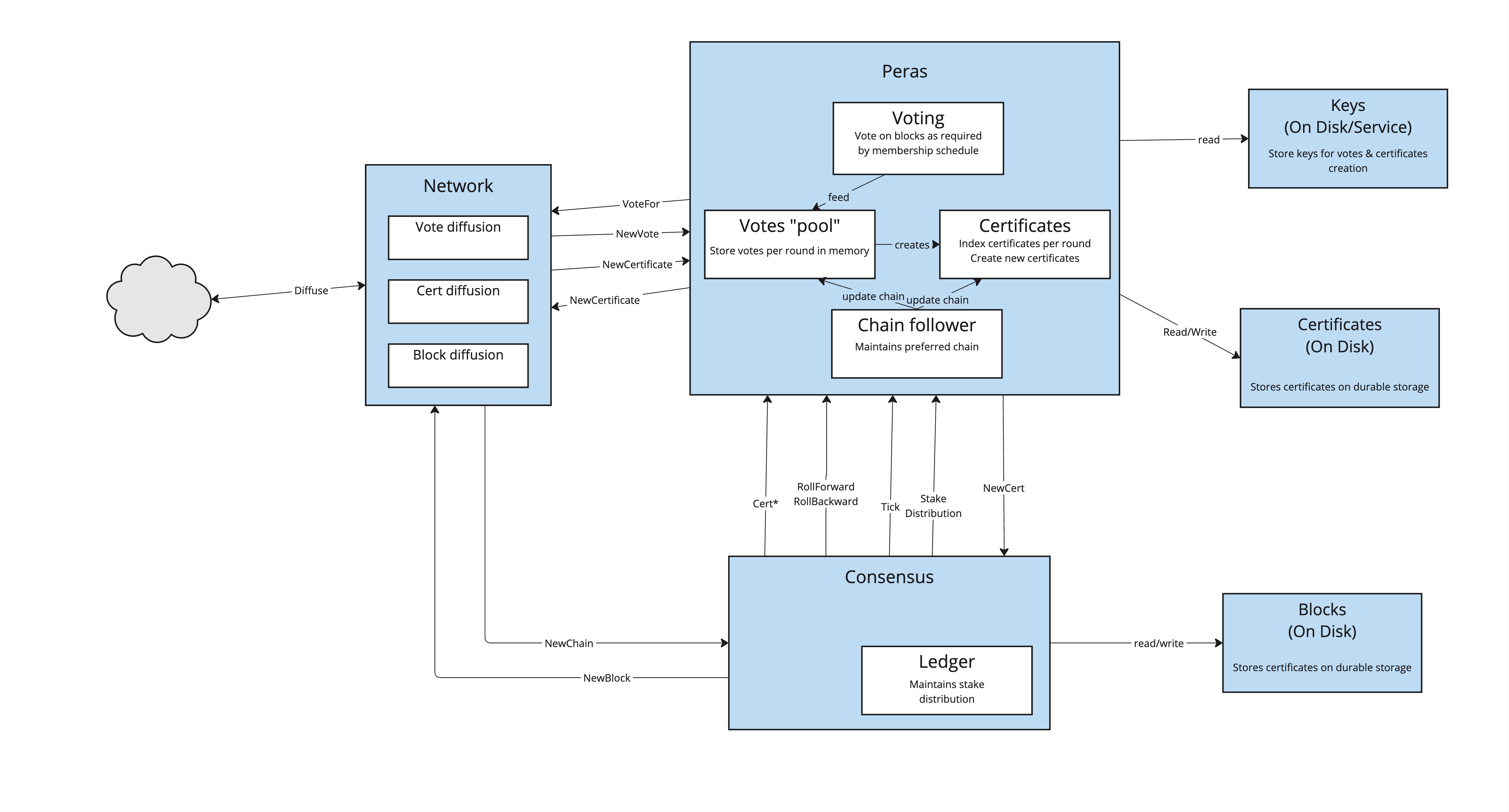
The main impacts identified so far are:

• There is no impact in the existing block diffusion process, and no changes to block headers structure.
• Block body structure needs to be changed to accomodate for a certificate when entering cooldown period.
• Consensus best chain selection algorithm needs to be aware of the existence of a quorum to compute the weight of a possible chain, which is manifested by a certificate from the Peras component.
  • Consensus will need to maintain or query a list of valid certificates (e.g., similar to volatile blocks) as they are received or produced.
  • Chain selection and headers diffusion is not dependent on individual votes.
• Peras component can be treated as another chain follower to which new blocks and rollbacks are reported.
  • Peras component will also need to be able to retrieve current stake distribution.
  • It needs to have access to VRF and KES keys for voting, should we decide to forfeit BLS signature scheme.
• Dedicated long term storage will be needed for certificates.
• Networking layer will need to accomodate (at least) two new mini-protocols for votes and certificates diffusion.
  • This seems to align nicely with current joint effort on Mithril integration.
• Our remarks regarding the possible development of a standalone prototype interacting with a modifified adhoc node still stands and could be a good next step.

Conclusion

The case for Peras

Peras provides demonstrably fast settlement without weakening security or burdening nodes. The settlement time varies as a function of the protocol-parameter settings and the prevalence of adversarial stake. For a use case that emphasizes rapid determination of whether a block is effectively finally incorporated into the preferred chain, it is possible to achieve settlement times as short as two minutes, but at the expense of having to resubmit rolled-back transactions in cases where there is a strong adversarial stake.

The impact of Peras upon nodes falls into four categories: network, CPU, memory, and storage. We have provided evidence that the CPU time required to construct and verify votes and certificates is much smaller than the duration of a voting round. Similarly, the memory needed to cache votes and certificates and the disk space needed to persist certificates is trivial compared to the memory needed for the UTXO set and the disk needed for the blocks.

On the networking side, our ΔQ studies demonstrate that diffusion of Peras votes and certificates consumes minimal bandwidth and would not interfere with other node operations such as memory-pool and block diffusion. However, diffusion of votes and certificates across a network will still have a noticeable impact on the volume of data transfer, in the order of 20%, which might translate to increased operating costs for nodes deployed in cloud providers.

In terms of development impacts and resources, Peras requires only a minimal modification to the ledger CDDL and block header. Around cool-down periods, a certificate hash will need to be included in the block header and the certificate itself in the block. Implementing Peras does not require any new cryptographic keys, as the existing VRF/KES will be leveraged. It will require an implementation of the ALBA algorithm for creating certificates. It does require a new mini-protocol for diffusion of votes and certificates. The node's logic for computing the chain weight needs to be modified to account for the boosts provided by certificates. Nodes will have to persist all certificates and will have to cache unexpired votes. They will need a thread (or equivalent) for verifying votes and certificates. Peras only interacts with Genesis and Leios in the chain-selection function and it is compatible with the historical evolution of the blockchain. A node-level specification and conformance test will also need to be written.

In no way does Peras weaken any of the security guarantees provided by Praos or Genesis. Under strongly adversarial conditions, where an adversary can trigger a Peras voting cool-down period, the protocol in essence reverts to the Praos (or Genesis) protocol, but for a duration somewhat longer than the Praos security parameter. Otherwise, settlement occurs after each Peras round. This document has approximately mapped the trade-off between having a short duration for each round (and hence faster settlement) versus having a high resistance to an adversary forcing the protocol into a cool-down period. It also estimates the tradeoff between giving chains a larger boost for each certificate (and hence stronger anchoring of that chain) versus keeping the cool-down period shorter.